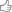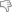-
.
Esistono numerosi prontuari dove trovare la freccia elastica di un particolare schema di trave, con varie ipotesi di vincolo di estremità, con differenti tipologie di carico.
Generalmente sono riportati i diagrammi dei tagli e dei momenti, e le frecce elastiche determinate nei punti 'singolari'. Ad esempio nell'ascissa di freccia massima, o in mezzeria, oppure all'estremità di un sbalzo.
Ma per quanto si possa possedere il prontuario più completo ed esaustivo ci sarà sempre il caso che voi state 'manipolando' e che sul prontuario non si trova.
Non bisogna andare nemmeno tanto lontano per ritrovarsi senza lo schema desiderato.
Qui ad esempio un caso da 'prefabbricatore', ovvero la trave ad inerzia variabile: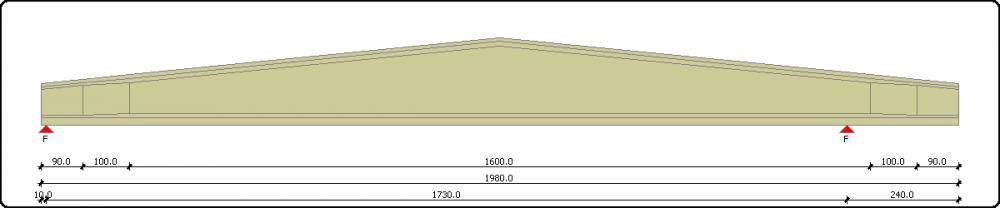
Variabile sia perchè ad altezza variabile, sia per i ringrossi e le rastremazioni di estremità.
Oppure casi di carico contemporaneo, che magari sono presenti singolarmente nel prontuario, ma in cui abbisogniamo della freccia in un punto ben preciso della trave e che non riscontriamo nel prontuario stesso: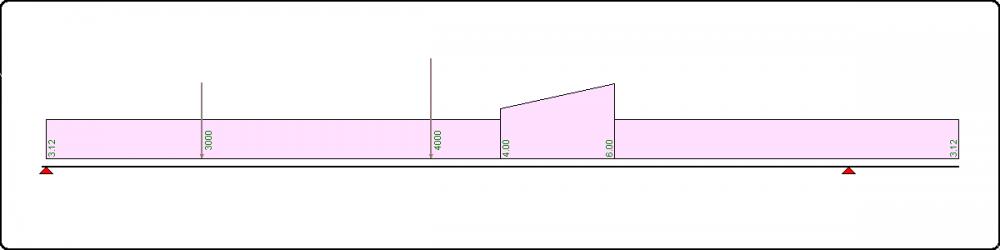
Oppure la trave continua con campate differenti, con inerzie diverse trave per trave, ecc.
Insomma, i casi della vita saranno sempre più numerosi di quanti possano essere contenuti nel prontuario più completo.
Quello che vi propongo è un metodo analitico 'esatto' (e lo metto tra virgolette per quanto dirò in seguito) che permette di affrontare tutti i casi che ho prospettato.
Si partirà sempre dalla equazione della linea elastica. Ma invece di procedere in modo tradizionale alla sua integrazione, vi propongo una sorta di metodo alle 'differenze finite'.
Il punto di partenza sarà l'equazione della linea elastica espressa in questa forma:
d²w(x)/dx²=-M(x)/E(x)·J(x)
Ovvero, per l'applicazione del metodo, bisognerà conoscere di già il diagramma dei momenti flettenti agente sulla nostra trave (singola, continua, con vincoli interni ed esterni dei più vari). E', in parte, una scocciatura. Ma questo consente di liberarsi, almeno per l'applicazione del metodo proposto, delle svariate tipologie di carico e di vincolo che possiamo riscontrare nella pratica.
Ho voluto aggiungere alla formula canonica le espressioni E(x) e J(x) semplicemente per puntualizzare il fatto che sia il materiale che la sezione possano avere variazioni lungo l'ascissa della trave (continue o discontinue, poco importa).
Tutto il 'trucco' del metodo consiste nel suddividere la nostra trave (o travata) in singoli conci elementari.
Guardiamo lo schema di figura in cui ci concentriamo sul singolo concio: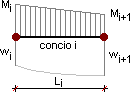
Il concio i avrà lunghezza Li, momento flettente all'estremo i pari ad Mi e momento flettente all'estremo i+1 pari ad Mi+1.
Parimenti il modulo elastico del materiale all'estremo i sarà pari a Ei ed all'estremo i+1 Ei+1
Anche per l'inerzia della sezione identicamente: Ji all'estremo i e Ji+1 all'estremo i+1.
Le estremità del nostro concio saranno 'accreditate' delle deformazioni elastiche (le nostre incognite) wi e wi+1
Per poter andare avanti nel nostro ragionamento dobbiamo fare le seguenti ipotesi:
1) Il momento flettente lungo la lunghezza Li del concio varia linearmente da Mi all'estremo i ad Mi+1 all'estremo i+1;
2) Il modulo elastico E del concio sarà costante e pari alla media tra Ei in i ed Ei+1 in i+1;
3) L'inerzia della sezione del concio sarà costante e pari alla media tra Ji in i ed Ji+1 in i+1;
Queste ipotesi rendono 'esatto' il metodo. Nel senso che più fittamente si suddivide la trave in conci, più la soluzione trovata si avvicinerà alla soluzione teorica esatta.
Le incognite del problema sono gli abbassamenti agli estremi di ogni singolo concio.
Non è affatto necessario che ogni singolo concio abbia identica lunghezza lungo la trave. Ma potrebbe essere opportuno che la suddivisione in conci debba seguire una logica.
Se voglio conoscere l'abbassamento della trave ad una ben precisa ascissa, questa deve essere estremo di uno dei conci in cui ho suddiviso la trave.
Oppure in base alla prima ipotesi (momenti variabili linearmente) la suddivisione in conci potrà essere svolta in modo da avere l'estremo di un concio posto in corrispondenza di una discontinuità del momento.
Nel prossimo post entreremo nel vivo.. -
.
A questo punto bisogna entrare dentro il singolo concio, integrando l'equazione della linea elastica.
Utilizzeremo una sorta di sistema di riferimento 'locale' del concio stesso, per cui l'ascissa x vale 0 nell'estremo i e varrà Li nell'estremo i+1.
Per la linearità dei momenti:
M(x)=Mi+(Mi+1-Mi)·x/Li
e si indichi con E ed J il modulo elastico medio e l'inerzia media del concio.
La nostra equazione diventa allora:
d²w(x)/dx²=-Mi/(E·J)-(Mi+1-Mi)·x/(Li·E·J)
Integriamola una prima volta, ottenendo:
dw(x)/dx=Ø(x)=-Mi·x/(E·J)-(Mi+1-Mi)·x²/(2·Li·E·J)+A
Ed infine una seconda volta per ottenere l'equazione della linea elastica del concio:
w(x)=-Mi·x²/(2·E·J)-(Mi+1-Mi)·x³/(6·Li·E·J)+A·x+B
Le costanti di integrazione A e B, come al solito, vanno determinate a partire dalle condizioni al contorno.
E quali sono queste condizioni?
Semplice. In corrispondenza della ascissa locale x=0 del concio la w(0) deve essere uguale a wi ed in corrispondenza di x=Li ,w(Li) deve essere uguale a wi+1
Dalla prima condizione si ricava che B=wi, dalla seconda invece:
wi+1=-Mi·Li²/(2·E·J)-(Mi+1-Mi)·Li²/(6·E·J)+A·Li+wi
E risolvendo, quindi:
A=(wi+1-wi)/Li+Mi·Li/(2·E·J)+(Mi+1-Mi)·Li/(6·E·J)
Adesso, sostituendo ad A e B le espressioni trovate abbiamo le equazioni del concio, sia per quanto riguarda le rotazioni che gli abbassamenti:
dw(x)/dx=Ø(x)=-Mi·x/(E·J)-(Mi+1-Mi)·x²/(2·Li·E·J)+(wi+1-wi)/Li+Mi·Li/(2·E·J)+(Mi+1-Mi)·Li/(6·E·J)
w(x)=-Mi·x²/(2·E·J)-(Mi+1-Mi)·x³/(6·Li·E·J)+[(wi+1-wi)/Li+Mi·Li/(2·E·J)+(Mi+1-Mi)·Li/(6·E·J)]·x+wi
Espressioni che si potrebbero anche ulteriormente semplificare. Ma solamente avendone voglia.
L'importante è che si capisca che le uniche incognite di queste 'articolate' espressioni sono.......
I momenti no. Quelli sono conosciuti e sono un dato del problema. Anche Il modulo elastico E e l'inerzia della sezione J la abbiamo definita a priori, quindi rimangono i veri 'colpevoli': wi e wi+1.
Ecco le vere incognite!
Vediamo alla prossima come ricavarle.. -
.
Appurato che le incognite siano le deformazioni agli estremi di ogni singolo concio, vediamo quali relazioni possiamo trovare al fine di determinarle.
Per far questo cominciamo ad 'unire' i vari conci tra loro.
Consideriamo ad esempio i primi due conci di una trave: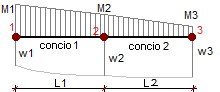
In corrispondenza del nodo 2 la rotazione del concio di sinistra, per congruenza, dovrà essere identica alla rotazione del concio di destra.
Ovvero, ricordando l'espressione della rotazione concio per concio, nel concio 1 la rotazione in 2 varrà:
Ø(L1)=-M1·L1/(E1·J1)-(M2-M1)·L1²/(2·L1·E1·J1)+(w2-w1)/L1+M1·L1/(2·E1·J1)+(M2-M1)·L1/(6·E1·J1)
E nel concio 2 la rotazione in 2 varrà:
Ø(0)=(w3-w2)/L2+M2·L2/(2·E2·J2)+(M3-M2)·L2/(6·E2·J2)
L'uguaglianza tra le due espressioni:
-M1·L1/(E1·J1)-(M2-M1)·L1²/(2·L1·E1·J1)+(w2-w1)/L1+M1·L1/(2·E1·J1)+(M2-M1)·L1/(6·E1·J1)=(w3-w2)/L2+M2·L2/(2·E2·J2)+(M3-M2)·L2/(6·E2·J2)
genera una equazione in cui compaiono le variabili w1, w2, w3 sempre e soltanto in termini lineari.
Potrei raggruppare tutto quanto, ottenendo un termine noto della singola equazione abbastanza 'nutrito' di elementi, e con un coefficiente -1/L1 per l'incognita w1, -1/L2 per l'incognita w3, e 1/L1+1/L2 per l'incognita w2.
Ma ciò che importa è che una simile equazione lineare può essere scritta per ogni nodo lungo la trave.
Se abbiamo una trave 'semplice' che è stata suddivisa in n conci, i nodi, compresi gli estremi, saranno in numero di n+1, e le equazioni che potremo scrivere saranno in numero pari ai nodi interni: n-1
Peccato, sembra che non possediamo un numero sufficiente di equazioni per determinare le nostre n+1 incognite.......
Ed invece no. Ci sono pure sempre le condizioni al contorno 'generali' della trave.
Perchè le deformazioni effettivamente incognite sono tutte quelle dei nodi non vincolati della trave. Per una trave con doppio appoggio (non importa se cerniere o incastri), senza dubbio la deformazione all'appoggio sarà nulla, o comunque un valore noto (caso di vincolo cedevole). Quindi non sarà una incognita.
Ed allora, riepilogando:
n-1 sono le equazioni;
n+1 sono i nodi totali lungo la trave;
2 sono però le deformazioni note;
ovvero le incognite sono in numero di n+1-2=n-1
Proprio come il numero di equazioni.
Quindi basta mettere a sistema tutte le equazioni per poter ricavare, con un qualsiasi algoritmo di risoluzione di sistemi lineari, tutte le deformazioni nodo per nodo in cui si è suddivisa la trave.
Qualcuno, che è riuscito a seguirmi bene, o che non è riuscito a seguirmi bene, potrebbe chiedersi a questo punto: ma per una semplice mensola, l'algoritmo proposto funziona, oppure no?. -
.Qualcuno, che è riuscito a seguirmi bene, o che non è riuscito a seguirmi bene, potrebbe chiedersi a questo punto: ma per una semplice mensola, l'algoritmo proposto funziona, oppure no?
Domanda d'esami?
Certo che funziona. Hai sempre due condizioni da poter imporre, ed entrambe al nodo incastrato; rotazione e abbassamento nulli.. -
.
Domanda:
come cambiare il suesposto algoritmo nel caso di una trave incastrata-appoggiata?
In questo caso avremmo:
n-1 sono le equazioni;
n+1 sono i nodi totali lungo la trave;
2 sono gli abbassamenti noti (nulli);
1 è la rotazione nota (nulla
ovvero le incognite sono in numero di n+1-2-1=n-2
Numero di equazioni n-1 e numero di incognite n-2.. -
.
Peccato......avevi superato l'esame, ero solamente indeciso sul voto finale......e mi vai a cadere sulla buccia di banana.
Il grado di vincolo 'rotazionale' degli estremi della trave è assolutamente ininfluente per l'algoritmo su esposto.
Questo non significa affatto che la deformata di una trave appoggio-appoggio venga fuori dall'applicazione dell'algoritmo uguale ad una trave incastro-appoggio.
Le condizioni al contorno nel secondo caso saranno identiche a quelle del primo caso, e saranno sempre: w1=0 e wn+1=0
Ricorda che l'algoritmo parte dalla conoscenza del diagramma dei momenti. Ed è il valore del momento in x=0 della trave che tiene già in conto, per la congruenza, del fatto che quel vincolo non ruota.
Quindi anche nel caso incastro-appoggio, o ancora: incastro-incastro, n-1 saranno le incognite, n-1 saranno le equazioni.
(Sempre per lo stesso motivo dico che l'algoritmo può esulare dalla trave 'semplice' e considerare travi con sbalzi e travi continue).. -
.Peccato......avevi superato l'esame, ero solamente indeciso sul voto finale......e mi vai a cadere sulla buccia di banana.
Con tutti questi spot fruttosi antirazzismo oggi è piu' facile che non ieri.CITAZIONEIl grado di vincolo 'rotazionale' degli estremi della trave è assolutamente ininfluente per l'algoritmo su esposto.
Ma da qualche parte dovrai pur imporre questo vincolo, altrimenti ricavi un abbassamento non corretto.. -
.
Come dicevo sopra, il vincolo viene da se.
Viene dalla forma del diagramma del momento flettente.
(e la forma del diagramma dei momenti, dipende ovviamente dalla tipologia dei vincoli). -
.Come dicevo sopra, il vincolo viene da se.
Viene dalla forma del diagramma del momento flettente.
(e la forma del diagramma dei momenti, dipende ovviamente dalla tipologia dei vincoli)
devo pensarci un po' sopra cercando di evitare le bucce.. -
.
@Zax
Io risolverei il problema da te proposto per travi qualsiasi in maniera più semplice col principio dei lavori virtuali, o principio degli spostamenti virtuali.
Data una trave di lunghezza [l], la dividiamo in [n] conci uguali, noto il modulo elastico [E],
trovo la freccia [delta] nel punto di ascissa [zv] con la routine di integrazione sottostante:CODICE'numero di suddivisioni trave per calcolare la freccia
Const n As Integer = 100
Dim Deltaz as double
Deltaz = l / n
Dim z as double
For i = 0 To n
'ascissa mobile [z]
z = (i * Deltaz)
'proprietà geometriche in corrispondenza della ascissa mobile [z]
calcola_prop_geom z, Jx
'Sollecitazioni dovute ai carichi agenti nella ascissa mobile [z]
Calcola_soll z, Mx
'Sollecitazioni dovute ad una forza concentrata unitaria nella ascissa di verifica [zv]
'valutate in corrispondenza della ascissa mobile [z]
Calcola_soll_Fv zv, 1#, z, M1
'freccia elastica [delta]
delta = delta + (Deltaz * Mx * M1) / (E * Jx)
Next i
Edited by texitaliano64 - 11/5/2014, 10:10. -
.
dougaj4 mi pare usi Macaulay nella sua UDF vettoriale... quindi direi la linea elastica no?
http://newtonexcelbach.wordpress.com/?s=conbeam. -
.
@Tex
Io ho proposto una 'mia' soluzione al problema. Però ho cercato di spiegare per bene da dove si parte, come si arriva al sistema risolvente e perchè (almeno lo spero).
Sto anche cercando, tempo permettendo, di creare un foglio di calcolo, stupido stupido, che ho già cominciato. E spero a breve (ma non prima di qualche giorno) di pubblicarlo.
Certo, dalla descrizione sembra una cosa complicata. Immagino ci siano 'sistemi' più semplici per arrivarci. E tra questi quello che tu proponi.
Ma perchè non lo espliciti meglio? Perchè non mi spieghi le basi teoriche senza le quali qualsiasi algoritmo non può essere implementato?. -
.
Il metodo delle differenze finite ha portata ampia, che mi pare il proposito d zax. Forse tex pensa al PLV applicato a una o poche travi. . -
.
Indovinato, io uso questa tecnica risolutiva per travette isostatiche.
@Zax
Il tuo metodo risolutivo lo trovo interessante, ma anche di complicata implementazione (risoluzioni di sistemi di equazioni chilometriche ed altre complicazioni).
Seguirò la tua implementazione con interesse, e possibilmente farò un foglio per il confronto numerico tra i due metodi da postare in questa sede.
L'algoritmo da me proposto per determinare la freccia in un punto qualsiasi della trave utilizza i cosidetti P.L.V.
Non mi dilungherò molto sulla descrizione del metodo poichè è spiegato nei testi di scienza delle costruzioni.
Nel campo delle strutture elastiche il principio dei lavori virtuali si impiega eguagliando i lavori esterno ed interno che un sistema di forze e azioni interne, fittizio ed equilibrato, opportunamente scelto ed applicato alla struttura, compie per effetto del sistema degli spostamenti e deformazioni reali di questa.
(lavoro virtuale esterno = lavoro virtuale interno)
Per l'applicazione del principio dei lavori virtuali, si sceglie il sistema fittizio costituito dalla forza unitaria applicata al punto della struttura di cui si ricerca lo spostamento e nella direzione di questo, in modo che per il lavoro esterno risulta una espressione molto semplice 1*delta.
L'espressione del lavoro virtuale interno è fornito da termini noti, sia azioni interne fittizie provocate dal carico unitario che deformazioni reali generate dal sistema di carichi esterni assegnato.. -
Renato T..
User deleted
Col PLV è inoltre molto semplice tener conto (contestualmente) delle deformazioni per taglio.
A mio avviso, in ogni caso, il problema principale di un sottoprogramma del genere consiste nell'assegnare in maniera efficiente e generale la variabilità delle sezioni. Personalmente opterei per una prima suddivisione in tronchi di trave; ogni tronco viene definito a mezzo delle due sezioni di estremità di tipo simile (assegnate ad esempio a mezzo delle coordinate trasversali che devono corrispondersi per numero di punti ordinati nella stessa modalità ad es. oraria). Ogni tronco viene a sua volta suddiviso in un numero intero di conci di uguale lunghezza (il più vicino possibile ad una prefissata mesh assegnata per l'intera trave).
I carichi distribuiti (ad esempio linearmente variabili) possono essere assegnati con riferimento ai suddetti tronchi. Lo stesso dicasi per eventuali carichi concentrati.
.
Un algoritmo 'duttile' per le frecce elastiche |