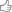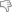-
|
| .
|
|
|
|
La ricerca degli zeri di una generica equazione può essere svolta in maniera numerica con metodi diversi.
I 'classici' metodi, cui spesso qui nei nostri algoritmi si ricorre, sono sostanzialmente tre.
A volte mi pare che li 'denominiamo' in maniera non corretta. Quindi mi sono imposto un piccolo ripasso.
Cominciamo con il "Metodo della corda":
Uno degli zero della funzione f(x) sia compresa nell'intervallo [A;B]
Il metodo consiste nel tracciare un segmento tra i punti A e B della curva. Una immagine dice meglio di tante parole.
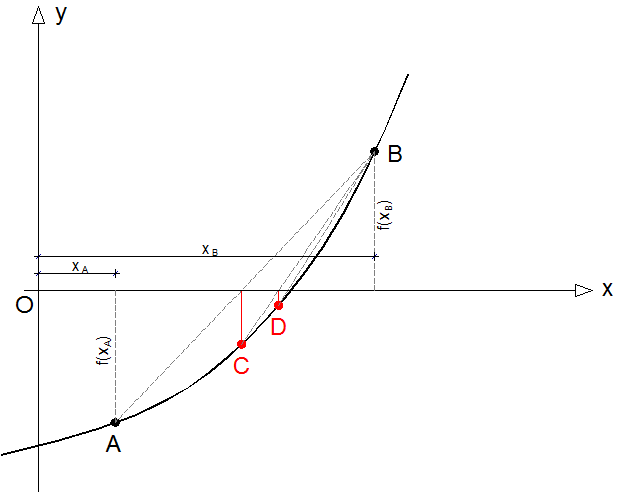
Il segmento tra A e B apparterrà alla retta con coefficiente angolare:
m=[f(xB)-f(xA)]/(xB-xA)
Nella forma canonica l'equazione della retta y=m·x+q passante per il punto B, assume la forma:
f(xB)=m·xB+q
E quindi:
q=f(xB)-m·xB
Intersecando con la retta y=0, l'ascissa del punto xC vale quindi:
xC=xB-f(xB)·(xB-xA)/[(f(xB)-f(xA)]
Determinata l'ordinata della funzione in xC si controllerà che f(xC) sia inferiore ad una data tolleranza (se questo accade, xC è la soluzione ricercata).
Se il valore f(xC) è maggiore della tolleranza si calcolerà, con l'espressione sopra vista la ascissa del punto D (questa volte nella formula al posto dell'indice A ci sarà l'indice C) e si controllerà se f(xD) sia inferiore alla tolleranza, altrimenti si ricaverà un ulteriore punto E e così via.
Edited by zax2013 - 4/12/2014, 19:27
|
|
|
| .
|
-
|
| .
|
|
|
|
Metodo della secante che consente una convergenza quadratica:
Assunti due valori iniziali x1, x2 per i quali f1=f(x1) ed f2=f(x2) abbiano segno opposto, si approssima la funzione f(x) a una retta passante tra i punti (x1,f1) e (x2,f2) assumendo come primo valore approssimato per x il punto dove la retta incontra l'asse delle x; il metodo equivale a un'interpolazione lineare.
Una semplice relazione di geometria elementare tra i due triangoli rettangoli simili, ricordando che f1 ed f2 hanno segno opposto, esprime la relazione:
CITAZIONE (x3-x1)/(x2-x3)=-f1/f2
Da cui, con brevi passaggi si ottiene un primo valore più approssimato dato dalla:
CITAZIONE x3=(x1*f2-x2*f1)/(f2-f1)
per il quale si calcola il valore della funzione f(x3).
La condizione iniziale del segno opposto non è indispensabile ma è utile perchè assicura la convergenza del metodo al valore ricercato.
Proseguendo a una seconda approssimazione, si assume il valore trovato per x3 come un nuovo valore iniziale e per il secondo si sceglie tra x1 e x2 quello per il quale la funzione ha segno opposto rispetto a f(x3); quindi se f(x3) ed f(x1) hanno segno opposto mantenendo x1 si pone x2=x3, se invece hanno lo stesso segno si sceglie x1=x3 mantenendo x2. Il metodo prosegue finchè non si raggiunge per f(x) un valore prossimo allo zero con la precisione richiesta.Attached Image
|
|
|
| .
|
-
|
| .
|
|
|
|
naturalmente quello che ha postato tex coincide con quello che ha postato zax, basta usare nella formula di zax la stessa notazione di tex e sviluppare il minimo comune multiplo.
ciò al fine di evitare, nel ripasso che stiamo facendo, che qualcuno possa essere tratto in inganno e pensare che si tratti di metodi diversi.
|
|
|
| .
|
-
|
| .
|
|
|
|
giusta precisazione quella di reversi.
ha tenuto conto della avanzata età di alcuni utenti...
o forse ha considerato che il post viene letto anche dai ragazzi delle medie?
|
|
|
| .
|
-
|
| .
|
|
|
|
Metodo delle secanti
Praticamente il metodo è assai simile a quello già visto per le corde, ed anche il motivo per cui spesso, come è successo a Tex, si faccia confusione.
Praticamente se nel metodo delle corde ad ogni iterazione il nuovo risultato si ricava avendo mantenuto fisso il punto A o B (nel mio esempio ho mantenuto fisso B), con il metodo delle secanti invece, ad ogni iterazione, il nuovo punto si ricava dai due precedenti (quindi alla iterazione n dalle coordinate dei punti n-1 ed n-2).
Al solito bisogna avere un intervallo di ricerca [A;B] all'interno del quale la funzione y=f(x) presenta uno zero reale.
Solito schemino:
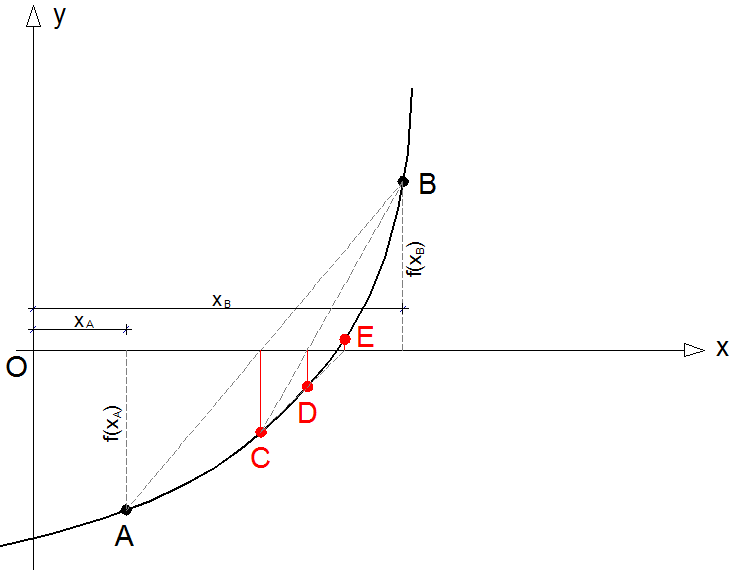
Quindi all'inizio si procede al solito modo. Tracciando il segmento tra A e B, e ricavando quindi la ascissa del punto C.
Il procedimento è assolutamente identico a quanto prima svolto, e quindi:
xC=xB-f(xB)·(xB-xA)/[(f(xB)-f(xA)]
Rispetto a quanto dice Tex non bisogna scegliere nulla. Bisogna solamente controllare che f(xC) non valga zero o valore inferiore alla tolleranza fissata, nel qual caso abbiamo trovato la soluzione.
Se ciò non accade secondo giro (segmento tracciato da C a B, intercettando sull'asse delle ascisse D):
xD=xC-f(xC)·(xC-xB)/[(f(xC)-f(xB)]
Anche qui, sembra non ci sia nulla di differente rispetto al metodo delle corde.
Ma se siamo costretti a fare una ulteriore iterazione, ecco che:
xE=xD-f(xD)·(xD-xC)/[(f(xD)-f(xC)]
Se guardate lo schema grafico di adesso, e quello del metodo delle corde di prima (volutamente ho lasciato più o meno la stessa curva) vedrete che in questa fase, il punto E con le secanti "è andato dall'altra parte" della curva rispetto al metodo delle corde (dove il punto E non l'ho segnato, ma avevo tracciato il segmento D-B).
Da quel punto in poi - con la curva del diagramma - la soluzione 'rimbalza' tra destra e sinistra dello zero, al contrario che con il metodo delle corde dove invece la soluzione anche all'ennesima iterazione (sempre per la curva del diagramma) rimane sempre a sinistra dello zero effettivo.
Questo 'rimbalzare' costituisce un vantaggio in termini di numero di iterazioni che risulterebbero in generale minori che non con il metodo delle corde.
Ma di questi aspetti parlerò - sempre ci riesca - in seguito.
|
|
|
| .
|
-
|
| .
|
|
|
|
CITAZIONE (zax2013 @ 5/12/2014, 14:15) Ma di questi aspetti parlerò - sempre ci riesca - in seguito.
ricordati che manca sempre una teoria, che di per sé già mancava...
|
|
|
| .
|
-
|
| .
|
|
|
|
CITAZIONE reversi
Inviato il 5/12/2014, 10:46
naturalmente quello che ha postato tex coincide con quello che ha postato zax, basta usare nella formula di zax la stessa notazione di tex e sviluppare il minimo comune multiplo.
ciò al fine di evitare, nel ripasso che stiamo facendo, che qualcuno possa essere tratto in inganno e pensare che si tratti di metodi diversi.
CITAZIONE (zax2013 @ 5/12/2014, 14:15) Metodo delle secanti
Praticamente il metodo è assai simile a quello già visto per le corde, ed anche il motivo per cui spesso, come è successo a Tex, si faccia confusione.
.....
Rispetto a quanto dice Tex non bisogna scegliere nulla. Bisogna solamente controllare che f(xC) non valga zero o valore inferiore alla tolleranza fissata, nel qual caso abbiamo trovato la soluzione.
Se ciò non accade secondo giro (segmento tracciato da C a B, intercettando sull'asse delle ascisse D):
.....
No non mi sono confuso Reversi e Zax quello che ho descritto è esattamente il metodo delle secanti.
Ribadisco che ogni metodo approssimato di calcolo numerico ha bisogno di avere un campo d'azione in cui trovare la radice.
Ora descrivo il metodo della bisezione:
Esistono molti metodi propri del calcolo numerico per interpolare via via i valori trovati e avvicinarsi a una soluzione con l'approssimazione voluta e il più rapidamente possibile. Un metodo molto semplice è quello della bisezione che richiede di individuare due valori x1 e x2 di x tra i quali sia sicuramente compresa una soluzione dell'equazione, il che equivale a dire che f(x1) e f(x2) devono avere segno opposto (cioè se f(x1)>0 allora f(x2)<0 e viceversa). Assumendo come nuovo valore quello intermedio:
si calcola il valore di f(x3) e si assume come nuovo intervallo di calcolo quello per il quale i due valori di f(x) hanno ancora segno opposto, proseguendo finchè il valore assoluto di f(x) è inferiore alla precisione richiesta.
|
|
|
| .
|
-
|
| .
|
|
|
|
Non avercela con noi Tex. Tu, rispetto ai metodi 'lisci' che io mi sto sforzando di descrivere, vai oltre inserendo delle condizioni che sicuramente dovrebbero portare alla soluzione con minori iterazioni. Condizioni che nei metodi 'originali' non ci sono, a scapito di una minore ottimizzazione (*).
Metodo delle tangenti
Conosciuto anche come metodo di Newton o di Newton-Raphson, avrebbe il merito di consentire la ricerca dello zero a partire da un solo punto iniziale, e non da due punti come nel caso del metodo delle corde o delle secanti.
La funzione y=f(x) dovrà essere derivabile (e la sua derivata differente da 0).
In pratica si tratta di tracciare a partire dal punto A della curva la retta tangente alla funzione y=f(x).
L'intersezione tra la retta tangente e l'asse delle ascisse costituisce ulteriore punto della iterazione.
Solito diagramma esplicativo:
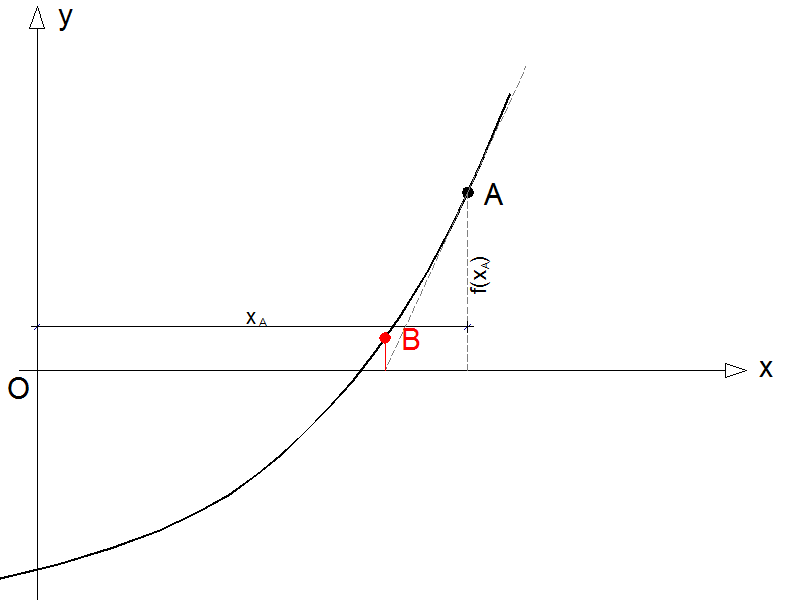
Come ben sappiamo il coefficiente angolare della retta tangente alla curva nel punto A è pari alla derivata prima della funzione stessa in A, ovvero:
m=f'(xA)
La retta passante per A e con coefficiente angolare m, nella forma canonica y=m·x+q dovrà avere:
q=F(xA)-m·xA
E quindi intersecando con l'asse delle ascisse tale retta troveremo il punto B di ascissa:
xB=xA-f(xA)/f'(xA)
Al solito, determineremo f(xB) verificando che essa valga zero o sia inferiore alla tolleranza fissata (quindi xB è la soluzione del nostro problema).
Se questo non accade ripeteremo il procedimento questa volta ricavando la derivata in B, trovando il punto C:
xC=xB-f(xB)/f'(xB)
E così via iterando.
Non vi nascondo che questo a me personalmente pare il metodo più bello ed elegante dei tre finora trattati.
Ovviamente bisogna pagare lo scotto: conoscere l'equazione della curva e la relativa derivata. E non incappare mai in un punto con derivata nulla.
(*) Ogni condizione inserita nei nostri algoritmi abbisogna di un tempo di elaborazione per controllare la condizione stessa.
A priori non possiamo generalizzare, in quanto il tempo complessivo di elaborazione dipende fortemente dalla espressione della curva.
E' probabile che per il controllo delle condizioni si possa impiegare più tempo che non ulteriori iterazioni, specie se le espressioni della curva non siano funzioni trigonometriche, ecc.
|
|
|
| .
|
-
|
| .
|
|
|
|
Come divertimento, ma anche per testare i tre metodi esposti, ho composto il foglio elettronico che metto in allegato a questo messaggio.
Ho introdotto una equazione di 5° grado, ne ho diagrammato lo sviluppo, e quindi ho utilizzato tutti e tre i metodi per determinare lo zero della funzione.
Come prevedibile, come letto altrove, il metodo delle corde si è rivelato il più inefficiente di tutti.
Con i dati 'originari' del foglio e con l'intervallo [A;B] prescelto bisogna ricorrere a 25 iterazioni per ottenere delle 'precisioni' che più o meno stiano in linea con gli altri due metodi.
Il metodo delle secanti, per quanto in fondo non si discosti da quello delle corde più di tanto (come abbiamo visto) riesce a 'stupirci' con sole 7 iterazioni.
Infine il metodo delle tangenti pare presentare una convergenza ancor più marcata con 5 sole iterazioni per arrivare alla soluzione.
Io ho provato a modificare l'intervallo [A;B] del foglio, anche mettendolo al di fuori dello zero (dal grafico più o meno so dove doveva trovarsi). Stranamente, ma immagino sia dovuto alla sostanziale 'monotonia' della funzione impostata, lo zero viene 'beccato' sempre e da tutti e tre i metodi.
Si modificano però, a volte anche di parecchio, il numero delle iterazioni. Ma questo fenomeno è molto più marcato per i primi 2 metodi (ma sempre la secante batte la corda).
Il metodo della tangente, che non risente di un intervallo, ma di un solo punto, alla fin fine (ma sarà stato un evento verificatosi per la particolare curva indagata) converge più o meno sempre nelle 5 iterazioni che vedrete nel foglio, rivelandosi il più 'stabile' al variare dei parametri tra i metodi esaminati.
Fate voi le vostre prove (file in formato Open/Libre Office)File Allegato
|
|
|
| .
|
-
|
| .
|
|
|
|
Voglio fare una precisazione.
Sembrerebbe dai metodi studiati, ma probabilmente ancor più fuori strada manda l'esempio che ho postato, che senza la conoscenza della espressione algebrica della funzione tali metodi non possano essere applicati.
In effetti non è vero.
Quello che importa è avere conoscenza 'puntuale' della funzione in corrispondenza di ognuno dei punti in cui iterando iterando si va a finire.
Questo implica comunque continuità della funzione, ecc.
Diciamo che è certamente così per i metodi di corde e secanti.
Per il metodo della tangenza, la conoscenza della derivata prima in effetti........fa cascare un pò l'asino.
Il topic sarebbe nato da Tex che ha ottimizzato un algoritmo di ricerca della effettiva posizione dell'asse neutro a rottura per sezioni generiche agli SLU.
Conosciamo l'espressione algebrica del problema? Ebbene, no.
Cosa abbiamo come 'ingrediente' in quel caso?
Posizioniamo l'asse neutro a 'casaccio' (sarebbe la nostra incognita x), e tramite una serie di elaborazioni ricaviamo lo sforzo normale che la sezione 'esplica' in una ben precisa configurazione di rottura (con quel posizionamento di asse neutro).
La differenza tra lo sforzo normale 'esplicato' e quello che effettivamente è lo sforzo normale agente sulla sezione risulterebbe essere la nostra incognita y, o per essere congruenti con la notazione qui utilizzata, f(xn).
Ecco quindi che basterà utilizzare, con uno dei primi due metodi, l'espressione:
xC=xB-f(xB)·(xB-xA)/[(f(xB)-f(xA)]
dove xC è la nuova posizione dell'asse neutro di tentativo, conoscendo nelle posizioni di tentativo xA ed xB la differenza dello sforzo normale (f(xA) ed f(xB)).
Tutto qui.
|
|
|
| .
|
-
|
| .
|
|
|
|
Scopro un metodo che non conoscevo.
Il metodo del punto unito
In pratica trovare gli zeri della funzione y=f(x) equivale a risolvere il sistema a due incognite:
y=f(x)
y=0
Adesso se ad entrambe le due equazioni sommiamo la variabile x, otteniamo:
y=f(x)+x
y=x
quindi se indichiamo con g(x) la prima equazione, e t(x) la seconda, il problema si riconduce a trovare le intersezioni tra queste due curve (la seconda una retta inclinata a 45° passante per l'origine, in realtà).
(pubblicherò dopo una immagine esplicativa)
Il criterio consiste nell'individuare un punto di primo tentativo x1, il secondo tentativo si ricava come x2=g(x1), il terzo come x3=g(x2), ecc.
Lo stop avviene quando xn+1-xn è inferiore ad una certa tolleranza.
|
|
|
| .
|
-
|
| .
|
|
|
|
il metodo appena postato da zax si generalizza ponendo:
y=f(x)+h(x)
y=h(x)
oppure se f(x) è scomponibile come somma algebrica di 2 funzioni f(x)=a(x)+b(x) in:
y=a(x)
y=-b(x)
esempio (banale):
gli zeri della funzione f(x)=x^3+x^2 sono dati dall'intersezione delle curve y=x^3 e y=-x^2
|
|
|
| .
|
-
|
| .
|

Junior Member

- Group
- Member
- Posts
- 13
- Reputation
- 0
- Status
- Offline
|
| |
Ciao a tutti...sono nuovo e avrei una curiosità in merito ai metodi per la ricerca degli seri. Nella procedura VCASLU del prof. Gelfi viene utilizzato il metodo ILLINOIS. Qualcuno è in grado di spiegarlo? Grazie
|
|
|
| .
|
-
-
|
| .
|
|
|
|
CITAZIONE (Mirkomachine @ 5/3/2019, 21:03) Nella procedura VCASLU del prof. Gelfi viene utilizzato il metodo ILLINOIS.
eccolo qua: https://en.wikipedia.org/wiki/False_position_method
per dare una veloce spiegazione, faccio l'esempio sul diagramma del primo post (metodo della corda).
unendo A e B trovo l'ascissa che mi consente di determinare C, che però non è ancora lo zero cercato.
a questo punto, dovrei vedere il segno di C per capire se al passaggio successivo devo unire C con A oppure con B.
siccome C ha il segno di A, devo unirlo con B.
il metodo illinois consente di abbreviare il tempo di convergenza poiché fa questa "osservazione": se C ha il segno di A, anche C/2 ha il segno di A, allora invece di usare C uso C/2 ed unisco questo con B.
proseguo perciò le successive iterazioni con questo stesso criterio.
è chiaro che invece di dividere per 2 posso decidere di dividere per 3 per 4 o per il numero che mi pare.
non è tutto oro quel che luce perché se la funzione non è monotòna possono aversi problemi.
il criterio qui sopra si può applicare anche ad altre procedure numeriche, non solo al metodo della corda.
Edited by reversi - 6/3/2019, 15:04
|
|
|
| .
|
15 replies since 4/12/2014, 19:12 1171 views
.