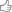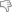|
|
|
Esistono numerosi prontuari dove trovare la freccia elastica di un particolare schema di trave, con varie ipotesi di vincolo di estremità, con differenti tipologie di carico.
Generalmente sono riportati i diagrammi dei tagli e dei momenti, e le frecce elastiche determinate nei punti 'singolari'. Ad esempio nell'ascissa di freccia massima, o in mezzeria, oppure all'estremità di un sbalzo.
Ma per quanto si possa possedere il prontuario più completo ed esaustivo ci sarà sempre il caso che voi state 'manipolando' e che sul prontuario non si trova.
Non bisogna andare nemmeno tanto lontano per ritrovarsi senza lo schema desiderato.
Qui ad esempio un caso da 'prefabbricatore', ovvero la trave ad inerzia variabile:
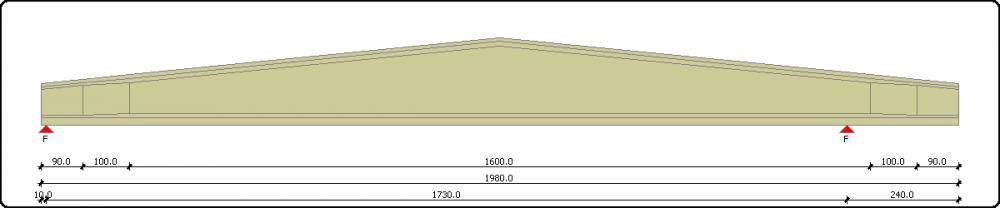
Variabile sia perchè ad altezza variabile, sia per i ringrossi e le rastremazioni di estremità.
Oppure casi di carico contemporaneo, che magari sono presenti singolarmente nel prontuario, ma in cui abbisogniamo della freccia in un punto ben preciso della trave e che non riscontriamo nel prontuario stesso:
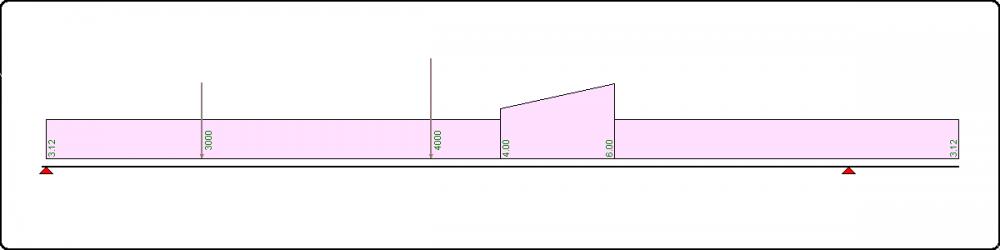
Oppure la trave continua con campate differenti, con inerzie diverse trave per trave, ecc.
Insomma, i casi della vita saranno sempre più numerosi di quanti possano essere contenuti nel prontuario più completo.
Quello che vi propongo è un metodo analitico 'esatto' (e lo metto tra virgolette per quanto dirò in seguito) che permette di affrontare tutti i casi che ho prospettato.
Si partirà sempre dalla equazione della linea elastica. Ma invece di procedere in modo tradizionale alla sua integrazione, vi propongo una sorta di metodo alle 'differenze finite'.
Il punto di partenza sarà l'equazione della linea elastica espressa in questa forma:
d²w(x)/dx²=-M(x)/E(x)·J(x)
Ovvero, per l'applicazione del metodo, bisognerà conoscere di già il diagramma dei momenti flettenti agente sulla nostra trave (singola, continua, con vincoli interni ed esterni dei più vari). E', in parte, una scocciatura. Ma questo consente di liberarsi, almeno per l'applicazione del metodo proposto, delle svariate tipologie di carico e di vincolo che possiamo riscontrare nella pratica.
Ho voluto aggiungere alla formula canonica le espressioni E(x) e J(x) semplicemente per puntualizzare il fatto che sia il materiale che la sezione possano avere variazioni lungo l'ascissa della trave (continue o discontinue, poco importa).
Tutto il 'trucco' del metodo consiste nel suddividere la nostra trave (o travata) in singoli conci elementari.
Guardiamo lo schema di figura in cui ci concentriamo sul singolo concio:
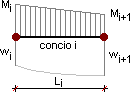
Il concio i avrà lunghezza Li, momento flettente all'estremo i pari ad Mi e momento flettente all'estremo i+1 pari ad Mi+1.
Parimenti il modulo elastico del materiale all'estremo i sarà pari a Ei ed all'estremo i+1 Ei+1
Anche per l'inerzia della sezione identicamente: Ji all'estremo i e Ji+1 all'estremo i+1.
Le estremità del nostro concio saranno 'accreditate' delle deformazioni elastiche (le nostre incognite) wi e wi+1
Per poter andare avanti nel nostro ragionamento dobbiamo fare le seguenti ipotesi:
1) Il momento flettente lungo la lunghezza Li del concio varia linearmente da Mi all'estremo i ad Mi+1 all'estremo i+1;
2) Il modulo elastico E del concio sarà costante e pari alla media tra Ei in i ed Ei+1 in i+1;
3) L'inerzia della sezione del concio sarà costante e pari alla media tra Ji in i ed Ji+1 in i+1;
Queste ipotesi rendono 'esatto' il metodo. Nel senso che più fittamente si suddivide la trave in conci, più la soluzione trovata si avvicinerà alla soluzione teorica esatta.
Le incognite del problema sono gli abbassamenti agli estremi di ogni singolo concio.
Non è affatto necessario che ogni singolo concio abbia identica lunghezza lungo la trave. Ma potrebbe essere opportuno che la suddivisione in conci debba seguire una logica.
Se voglio conoscere l'abbassamento della trave ad una ben precisa ascissa, questa deve essere estremo di uno dei conci in cui ho suddiviso la trave.
Oppure in base alla prima ipotesi (momenti variabili linearmente) la suddivisione in conci potrà essere svolta in modo da avere l'estremo di un concio posto in corrispondenza di una discontinuità del momento.
Nel prossimo post entreremo nel vivo.
|
|