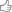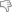-
|
| .
|
|
|
|
Cosa sono i quaternioni ?
Edited by afazio - 7/4/2016, 12:49Attached Image
|
|
|
| .
|
-
|
| .
|
|
|
|
Per quanto riguarda le rotazioni nello spazio 3D, oggi cercando la formula di Rodrigues mi sono imbattuto sui Quaternioni.
Approfondendo la lettura su questi strani oggetti ho scoperto che sono utilizzati nella computer graphics per operare una qualsiasi rotazione di un vettore 3D attorno ad un asse 3D di un qualunque angolo alfa.
IL quaternione è una struttura numerica complessa simile ai numeri complessi, ma sono ancora più complessi dei numeri complessi che conosciamo, ed appunto per questo possono anche essere denominati "numeri IperComplessi".
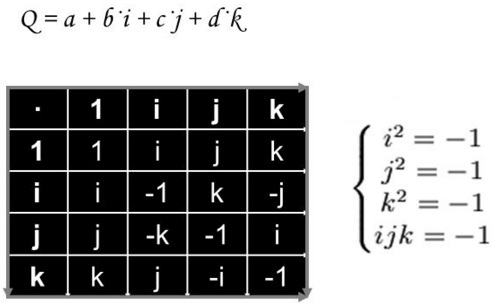
In analogia al numero complesso che conosco z= a +i*b il quaternione è definito da
q= a + i*b + j*c + k*d
in cui i simboli i, j, k possono essere visti come entità immaginarie oppure come versori degli assi di una terna xyz in 3D.
Hamilton, che fu il primo che li studiò, fissò delle regole principali per poter operare con queste strane cose, come per esempio:
i²=j²=k²=i*j*k=-1
oltre alle regole:
i*j = k (j*i=-k)
j*k= i (k*j=-i)
k*i= j (i*k=-j)
Cosi come i numeri complessi possono scriversi nella forma z=( a ; i*b)
anche i quaternioni possono scriversi nella forma q=(a ; ib; jc, kd)
similmente per la scrittura nella forma esponenziale o nella forma trigonometrica.
esistono particolari tipi di quaternioni che permettono di eseguire la rotazione di un vettore in un battibaleno.
|
|
|
| .
|
-
|
| .
|
|
|
|
Un vettore nello spazio 3D puo' essere espresso come combinazione lineare dei versori degli assi:
v = b*i + c*j +d*k
riprendendo la forma del quaternione
q = a + b*i + c*j +d*k
avremo q= a + v
Sotto questo punto di vista, il quaternione puo' definirsi come una struttura complessa costituita dalla somma di un reale con un vettore.
Possiamo quindi scrivere il quaternione anche come:
q = [ a; v]
Si definisce coniugato del quaternione
q = a +b*i + c*j +d*k,
il quaternione
q* = a -b*i - c*j -d*k
o in altra forma
q* = [ a; -v]
Edited by afazio - 18/8/2013, 22:41
|
|
|
| .
|
-
|
| .
|
|
|
|
Similmente ai numeri complessi, anche coi quaternioni vengono definite le varie operazioni come:
somma
differenza
prodotto
divisione
modulo o norma
quaternione reale
quaternione immaginario (o vettore puro)
quaternione unitario
coniugato
In particolare il modulo di un quaternione q = [a; v] è definito come
|q²|= a² +|v²| = a² +b² + c² +d²
o anche
|q| = q*q' =q'*q
in cui ho indicato con q' il coniugato di q
Se la norma di un quaternione è pari ad uno, il quaternione si dice essere unitario.
E sono proprio i quaternioni unitari che diventano gli operatori della rotazione in 3D di un qualsiasi vettore rispetto ad un asse e di un angolo a piacimento.
|
|
|
| .
|
-
|
| .
|
|
|
|
Un quaternione unitario, quello che ci interessa nelle rotazioni, è:
q= [ cosϑ ; n*sinϑ]
in cui n è un vettore di modulo unitario avente quindi le tre componenti
nx = b*i/radq(b²+c²+d²)
ny = c*j/radq(b²+c²+d²)
nz = d*k/radq(b²+c²+d²)
Dato adesso un generico vettore p=[px ; py; pz]
o scritto anche nella forma p = i*px + j*py+k*pz
esso puo' essere visto come un quaternione con la parte reale nulla
qp = [ 0; p]
ed ecco adesso la magia:
Il prodotto q*qp*q' produce la rotazione del vettore p dell'angolo 2*ϑ rispetto all'asse definito da n
indicando quindi con w il vettore che si produce dopo la rotazione, avremo:
[0; w] = [ cosϑ ; n*sinϑ]*[ 0; p]* [ cosϑ ;- n*sinϑ]
Modificando il quaternione unitario in
q= [ cosϑ/2 ; n*sinϑ/2] otterremo una rotazione di ϑ
Quindi è sufficiente conoscere le regole della moltiplicazione tra quaternioni per ottenere il vettore ruotato nello spazio 3D.
Si definisce un operatore M una volta per tutte che applicato ad un vettore produce la rotazione voluta.
w=M*p
l'operatore M è meglio illustrato nella seguente immagine tratta da un documento trovato in rete

L'unica nota esplicativa alla formula riportata nell'ìmmagine è che l'inverso di un quaternione unitario coincide con il coniugato.
Edited by afazio - 19/8/2013, 00:06
|
|
|
| .
|
-
|
| .
|
|
|
|
La mia curiosità mi ha spinto a provare a vedere come applicare i quaternioni nelle rotazioni.
In sostanza si tratta di costruire la matrice M dati l'asse di rotazione n e l'angolo ϑ di rotazione.
Il problema fondamentale è che purtroppo non è facile avere una visione 3D di ciò che succede guardando come variano le componenti del vettore che intendo ruotare e non posseggo strumenti in grado di fornirmi una rappresentazione tridimensionale. Dovrei fare ricorso al modulo 3D di autocad ma non sono sicuro di riuscire a tirarci fuori qualcosa.
Ho però pensato che se la cosa vale in 3D varrà anche in 2D considerando un piano coordinato (per esempio il piano xy). Intanto vediamo che succede nel caso piano.
Ho considerato un vettore nel piano xy di modulo pari a 2 ed inclinato di 15° rispetto all'asse delle x misurati in senso orario.

Adesso intendo ruotare il vettore dato attorno all'asse z una volta di 15° in senso antiorario ed una volta di 15° in senso orario.
Nel primo caso mi aspetto che il vettore risultante a rotazione avvenuta sia:
wx=2*i
wy=0
wz=0
nel secondo caso
wx= 2*cos(30)* i = 1.732*i
wy=-2*sen(30)*j = -1.00 *j
wz=0
Per prima cosa mi costruisco il quaternione unitario nella forma espressa nell'immagine del post precedente, e cioè:
q=[ s; (x,y,z)]
questo deriva dalla forma:
q=[cosϑ/2 ; n*senϑ/2]
ma avendo assunto come asse di rotazione l'asse z avremo:
n=[0; 0 ; 1]
essendo anche
senϑ/2 = 0.1305
cosϑ/2 = 0.9914
il quaternione unitario che opera la rotazione di +15° diviene:
q=[0.9914 ; 0 ; 0 ; 0.1305]
quindi abbiamo:
s=0.9914
x=0
y=0
z=0.1305
Con questi dati possiamo costruirci l'operatore M

Scriviamo adesso il vettore v che intendiamo ruotare:
secondo quanto scritto precedentemente, esso dovrebbe essere espresso sotto forma di quaternione con parte reale nulla, quindi
qv=[ 0; 1.932; -0.518; 0]
e quindi trovare il quaternioneqw (espresso sempre sotto forma di quaternione con parte reale nulla) applicando a qv l'operatore M, cioè
qw = M*qv
Ma cosi facendo le cose non tornano affatto. Sono quindi andato a rileggere il documento da cui ho tratto quel che ho riassunto nel topic ed ho compreso che per poter applicare l'operatore M scritto in quella forma i quaternioni dei vettori v e w vengono scritti nella forma alternativa:
qv =[v; 0]
qw =[w; 0]

Rimane pertanto da eseguire il prodotto tra unamatrice 4x4 ed un vettore 4x1.

Il risultato ottenuto è quanto mi aspettavo.
Nella immagine che segue sono invece riassunti i passi per la rotazione di -15°

Anche in questo caso il risultato è quello atteso.
Guardando meglio la matrice M, ho visto che è possibile ridurla ad una matrice 3x3 togliendo l'ultima riga e l'ultima colonna ed applicarla direttamente al vettore v senza doverlo esprimere sotto forma di quaternione ottenendo il vettore w nella forma vettoriale.
|
|
|
| .
|
-
|
| .
|
|
|
|
Aggiungiamo un minimo di tridimensionalità all'esempio precedente.Consideriamo che il vettore dato sia la proiezione sul piano xy di un vettore spaziale la cui terza componente vale 1.50*k

Stavolta vogliamo ruotare il vettore di +15° e di -75°
Ci aspettiamo che la componente z del vettore rimanga sempre pari ad 1.50.
Nel primo caso ci aspettiamo come risultato della rotazione il vettore:
w=[ 2 ; 0 ; 1.50]
mentre nel secondo caso
w=[ 0; -2 ; 1.50]
Ed infatti è proprio cosi. ecco le due schermate relative a:
rotazione del vettore di +15°

rotazione del vettore di -75°

Edited by afazio - 19/8/2013, 17:58
|
|
|
| .
|
-
|
| .
|
|
|
|
E cosa accade se ruotiamo il vettore dato
v=[1.932 ; -0.518 ; 1.500]
attorno a se stesso di un qualsiasi angolo?
Naturalmente la risposta è banale: il vettore deve restare immutato. Ma vediamo se l'applicazione dell'operatore M produce proprio questo risultato.
Per prima cosa dobbiamo determinarci le componenti dell vettore unitario n che rappresenta la direzione del vettore dato e per questo ci serve la norma di v.
|v| = radq( 1.932² +0.518² + 1.50²) = 2.50
quindi abbiamo
n = [ 1.932/2.50 ; -0.518/2.50 ; 1.50/2.50 ] = [0.773 ; -0.207 ; 0.600]
fissiamo un angolo di rotazione ϑ=30°
scriviamo quindi il quaternione unitario relativo a ϑ ed n e quindi ci costruiamo la matrice M.
A questo punto eseguiamo il prodotto M*v ed otteniamo il risultato aspettato.
ecco la schermata tratta dal foglio excel che ho predisposto.

Mi ritengo soddisfatto anche se rimane ancora qualche altro aspetto da puntualizzare sulle rotazioni di figure 3D.
|
|
|
| .
|
-
|
| .
|
|
|
|
Fino ad adesso si è trattato di vettori generici senza alcun punto di applicazione. Infatti il vettore da ruotare è dato attraverso le sue tre componenti che rimangono uguali traslando il vettore parallelamente a se stesso in qualsiasi punto dello spazio.
L'applicazione dell'operatore M al vettore v=[vx; vy; vz] produce una rotazione attorno all'asse n del quaternione di rotazione e passante per il punto di applicazione del vettore stesso.
Quindi se il vettore viene dato attraverso le coordinate dei suoi due estremi AB, l'applicazione di M a v = [(xB-xA) ; (yB-yA) ; (zB-zA)] produce una rotazione sempre attorno all'asse n passante per il punto A e non attorno all'asse n passante per l'origine degli assi.
Come operare allora se vogliamo che la rotazione avvenga rispetto all'asse n passante per un prefissato punto P dello spazio?
Occorre prima operare una traslazione degli assi portando l'origine del nuovo sistema sul punto P e quindi operare la rotazione dei vettori PA e PB applicando ad entrambi l'operatore M. A questo punto riportiamo gli assi nel punto originario ed avremo le coordinate dei due punti di estremità del vettore AB ruotato.
|
|
|
| .
|
-
|
| .
|
|
|
|
Smanettando con le rotazioni mediante i quaternioni ho visto che la rotazione dell'angolo ϑ attorno all'asse n equivale alla rotazione di -ϑ attorno all'asse -n.
In altre parole significa che cambiare il verso di n equivale a cambiare il segno di ϑ mantenendo n immutato.
|
|
|
| .
|
9 replies since 18/8/2013, 09:57 471 views
.