-
.
In questo topic intendo riportare tutti gli aspetti teorici che hanno portato alla scrittura di parecchio codice circa la verifica di sezioni presso inflesse di forma generica in c.a.
Non me ne vogliate del fatto che sarebbe una mera ripetizione di quanto a partire da Marzo del 2011 avevo già svolto qui:
Programma di verifica a presso-flessione deviata di sezioni generiche in c.a.
Il fatto è che nel settembre del 2012, afazio ha iniziato questo topic:
Verifiche sezioni complesse in c.a. agli SLE ed SLU
Dando per scontate tutte le considerazioni teoriche che avevano portato alla scrittura di codice in C che lui si apprestava a tradurre in VBA in modo da incorporare le varie routine in Excel.
Non aveva tutti i torti, visto che buona parte di noi frequentatori di questo forum 'deriviamo' in qualche modo da ingegneriaforum.it (e quindi avevamo letto il topic lì sviluppato).
Ma la mia impressione, specie con il passare del tempo, è stata che nel topic iniziato da Afazio il codice non è..... come dire.....ben commentato.
Qualche nuovo utente che nei prossimi anni qui al Bar dovesse imbattersi nella discussione di cui sopra potrebbe non capire bene.
E' molto più importante, a detta di tutti, capire come funziona il meccanismo, piuttosto che copiare le righe e piazzarle in un qualsiasi ambiente di sviluppo.
L'iniziativa di Afazio ha comportato un certo 'fiorire' di discussioni 'corollario', io ho raccolto queste, (se ne ho dimenticata qualcuna, ditemi ed aggiungerò):
Ci.A.Pi.
La DLL-ificazione dello ZaxCode
Algoritmi - Quattro passi sui quattro vertici
Nonchè anche qualche discussione un pò più 'pepata' come questa:
Quer pasticciaccio brutto....
Che, forse, ha comportato il volontario allontanamento di un 'pezzetto' importante di forum.
Dal prossimo post si entrerà nel vivo. Spero di essere meno prolisso di quanto non sia stato la prima volta. Sono indeciso se riportare anche gli stralci di codice, oppure 'rimanere' alla sola pura e semplice teoria.. -
.
Parte 1
Geometria della sezione e sue caratteristiche geometriche
Per prima definiamo cosa intendiamo per sezione di forma generica.
Le sezioni che andremo ad esaminare avranno forma poligonale.
Dato un insieme n di punti, le cui coordinate siano riferite ad un sistema cartesiano, si individua una sequenza dei vertici stessi in modo che il vertice 1 venga unito da un segmento al vertice 2 che verrà quindi unito con altro segmento al vertice 3, e così via fino all'ultimo vertice.
Unendo infine il primo vertice della sequenza con l'ultimo si ottiene un poligono chiuso (ma che non dovrà essere intrecciato).
Ecco cosa si intende: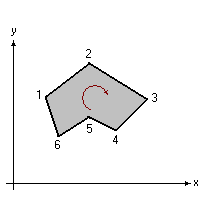
Riguardo eventuali parti curvilinee della sezione queste potranno essere “riprodotte” con opportuni raffittimenti di vertici che approssimeranno più o meno bene queste parti. Ma in ogni caso comunque la sezione rimane poligonale.
Per quello che sarà lo svolgimento successivo e per le formulazioni che verranno esposte è opportuno che la sequenza dei vertici uniti dai segmenti sia data in senso “orario” (così come nell'immagine).
La realtà generalmente non è così semplice. Una sezione di forma realmente generica infatti può essere costituita da parti piene e parti vuote, oppure da porzioni di sezione fatte con differente materiale (esempio sezioni precompresse con soletta di differenti caratteristiche del calcestruzzo, oppure sezioni in acciaio-calcestruzzo, ecc.).
Quindi se vogliamo mantenere generalità, la sezione potrà essere rappresentata non da uno, ma da più poligoni.
Per quanto riguarda il calcolo delle caratteristiche geometriche ci concentreremo al momento su un singolo poligono. Va da se che quanto si svilupperà potrà essere esteso all'insieme di più poligoni.
Premetto che queste nozioni di base sono finalizzate al calcolo SLE delle sezioni.
Il calcolo delle caratteristiche geometriche di una sezione rappresentata da un poligono, baricentri, momenti statici e di inerzia rispetto agli assi coordinati, viene svolto scomponendo il poligono in trapezi elementari ed utilizzando una sommatoria di momenti statici e di inerzie riferite ad un singolo segmento alla volta del poligono stesso.
Nelle due immagini sottostanti potete vedere cosa si intende: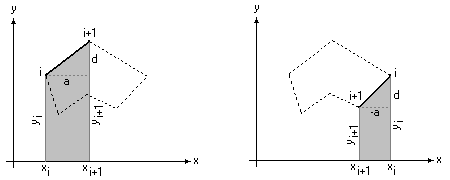
E' semplice verificare cosa accade se vogliamo calcolare l'area del poligono. Basterà calcolare l'area del trapezio sotteso ad ogni segmento (quello in grigio nella figura), per capire, girando segmento per segmento del poligono, fino all'ultimo segmento che unisce l'ultimo vertice con il primo, che alcuni trapezi avranno area positiva (ad esempio quello segnato), altri area negativa (quello della seconda immagine, perchè x[i+1]-x[i] diventa negativo), e pertanto la somma algebrica di tutte queste aree restituisce, appunto, l'area del poligono.
Per le altre caratteristiche geometriche, si procederà in maniera analoga.
Il problema “elementare” quindi sarà calcolare le caratteristiche geometriche del trapezio segnato nelle figure.
In questo modo comunque tutte le caratteristiche geometriche saranno riferite al sistema di riferimento prescelto, e quindi, almeno per i momenti statici e di inerzia, agli assi x ed y di figura.
Poco male. Basterà utilizzare i teoremi di trasporto per ritrovare momenti statici ed inerzie riferiti al baricentro della sezione. Perchè è questi che di seguito ci interesseranno.
Allora, per semplificare le varie formule si è indicato con a il valore (x[i+1]-x[i]) e con d il valore (y[i+1]-y[i]). In questo modo l'area sarà la somma di un rettangolo e di un triangolo (anche di area negativa se d è negativo), ed anche i momenti statici e le inerzie verranno spezzettate sommando inerzie di rettangoli e triangoli.
In definitiva avremo:
area
a*y[i]+a*d/2 --> ovvero semplificando: a*(y[i]+d/2)
momento statico attorno all'asse x
a*y[i]2/2+a*d/2*(y[i]+d/3) --> ovvero semplificando: a/2*(y[i]2+d*2/3+d*y[i])
momento statico attorno all'asse y
In questo caso dovete immaginare il trapezio disposto in verticale proiettando il segmento sull'asse y, piuttosto che sull'asse x.
-d*x[i]2/2+d*a/2*(x[i]+a/3) --> ovvero semplificando: -d/2*(x[i]2+a2/3+a*x[i])
momento d'inerzia attorno all'asse x
a*y[i]3/3+a*d3/36+a*d/2*(y[i]+d/3)2 --> ovvero semplificando: a/3*(y[i]3+y[i]*d2+3*y[i]2*d/2+d3/4)
momento d'inerzia attorno all'asse y
Anche in questo caso il trapezio è ruotato, proiettando il segmento sull'asse y.
-d*x[i]3/3+d*a3/36+d*a/2*(y[i]+a/3)2 --> ovvero semplificando:
-d/3*(x[i]3+x[i]*a2+3*x[i]2*a/2+a3/4)
momento d'inerzia xy
a*(x[i]/2*(y[i]2+d2/3+d*hy)+a/2*(y[i]2/2+d2/4+2*d*hy/3))
Adesso, ottenute tutte queste grandezze, sommandole tra loro, segmento per segmento costituente il poligono, ed eventualmente ripetendo ancora l'operazione per gli altri poligoni che compongono la sezione è possibile trovare il baricentro della sezione:
xg=Mstaticoy/Atot
yg=Mstaticox/Atot
Ed una volta avuto il baricentro, con i vari teoremi di trasporto ricavare le inerzie. Ad esempio:
Jxg=Jx-Atot*yg2
E così via.
Personalmente ho sempre avuto qualche difficoltà proprio in questa fase, specie per l'inerzia xy.
La mia personale soluzione, allungando un po' il brodo, è stato di calcolare prima aree e momenti statici, in modo da determinare inizialmente i baricentri, ed infine calcolarmi le inerzie direttamente dal baricentro (con una banale traslazione degli assi).
Per completare questa prima parte introduciamo anche il valore di alfa, ovvero l'angolo degli assi principali di inerzia rispetto agli assi coordinati, ed i valori dei momenti principali di inerzia rispetto agli assi principali.
Come in tutti i manuali di geometria delle masse:
alfa=atan(-2*Jgxy/(Jgx-Jgy))/2
Jalfa=(Jgx+Jgy)/2+sqrt((Jgx-Jgy)2+4*Jgxy2)/2
Jbeta=(Jgx+Jgy)/2-sqrt((Jgx-Jgy)2+4*Jgxy2)/2
Preciso che per lo specifico problema che intendiamo affrontare, la verifica SLE o SLU delle sezioni, e con gli algoritmi presentati, queste ultime grandezze (inclinazione degli assi principali e relative inerzie) non verranno mai utilizzate.
Edited by zax2013 - 1/3/2014, 20:00. -
.
Parte 2
Coefficiente di omogeneizzazione ed armature
Si era fatto un semplice accenno a sezioni costituite da differenti poligoni, poiché costituite da differenti materiali. Nel determinare le caratteristiche geometriche della sezione però nelle formule presentate non vi è alcun riferimento a tale aspetto. Ogni poligono sembrerebbe venir trattato allo stesso modo.
Introduciamo quindi un numero per ogni poligono da applicare come semplice moltiplicatore alle caratteristiche geometriche dello stesso (area, momenti statici, inerzie).
Ovviamente, lo vedremo in seguito, questo numero avrà un senso fisico, e ci permetterà di studiare, agli SLE, sezioni costituite da differenti materiali.
Vediamo invece come sia possibile con questo moltiplicatore gestire un eventuale vuoto interno alla sezione. Esso verrà rappresentato al solito da un poligono e potrà essere trattato come tutti gli altri poligoni costituenti la sezione, ma assegnando un fattore moltiplicativo negativo al poligono che lo rappresenta.
Valore negativo che potrà essere -1 o un valore differente.
Un esempio 'articolato' chiarirà meglio.
Immaginate di avere una sezione precompressa, cava, che viene completata in opera, con un getto di calcestruzzo di differenti caratteristiche meccaniche, a sua volta cavo, perchè alleggerito con del polistirolo.
Ecco, per rappresentare una simile sezione occorreranno 4 poligoni. Un primo poligono sarà la parte “esterna” della sezione in c.a.p., il secondo poligono, la parte “vuota” della stessa, un terzo poligono il contorno esterno del getto in opera, ed infine il quarto poligono il vuoto all'interno della soletta.
Il calcestruzzo della trave e della soletta sono differenti. Ma essi possono essere trattati come se fossero uno solamente introducendo il fattore n di omogeneizzazione (il nostro moltiplicatore) dato dal rapporto tra i moduli elastici dei due calcestruzzi.
Tale moltiplicatore può valere ad esempio 1.0 per il poligono “pieno” esterno della sezione in c.a.p., -1.0 per il poligono che rappresenta il “vuoto” della sezione predetta, valere (esempio) 0.79 per il poligono che rappresenta la parte esterna della soletta, ed infine -0.79 per la sua parte “vuota”.
Allo stesso modo, con l'utilizzo di un moltiplicatore, verranno introdotte le armature nella determinazione delle caratteristiche geometriche delle sezioni. Tale moltiplicatore avrà il 'classico' valore di 15, oppure il valore ritenuto opportuno.
Ogni singola barra di armatura verrà considerata come una massa concentrata disposta nelle coordinate x,y e di area af. Ossia come in figura: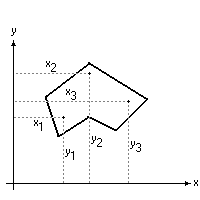
In questo modo le varie entità geometriche già viste nella parte 1, dovranno essere aumentate delle quantità, calcolate barra per barra:
area
omog*af
momento statico attorno all'asse x
omog*af*y[i]
momento statico attorno all'asse y
omog*af*x[i]
momento d'inerzia attorno all'asse x
omog*af*y[i]2
momento d'inerzia attorno all'asse y
omog*af*x[i]2
momento d'inerzia xy
omog*af*x[i]*y[i]
Prima di apprestarci a trattare le verifiche, è opportuna una puntualizzazione.
Generalmente le sollecitazioni di verifica di una sezione derivano da un 'problema più grande'. Come minimo stiamo esaminando un elemento monodimensionale (una trave, una colonna). Tale elemento viene in ogni caso schematizzato con il suo asse. Asse passante per i baricentri delle sezioni dell'elemento.
Pertanto le sollecitazioni che derivano da una analisi strutturale articolata hanno come 'polo' il baricentro della sezione.
Finchè trattiamo la sola flessione questa precisazione è di fatto inutile. Ma quando introduciamo anche lo sforzo normale il punto di applicazione della risultante va definito.....rispetto a cosa? Rispetto al baricentro della sezione.
Nel proseguo di questa trattazione il baricentro della sezione sarà quello definito senza la presenza delle armature.
(Le armature possono modificare il baricentro della sezione, modificando anche le sollecitazioni da calcolo che non derivano più da uno schema geometrico congruente). -
.
Parte 3
Verifica a presso-flessione agli SLE
Si procede inizialmente con sezioni di forma generica qualsivoglia ma con tutti i poligoni reagenti sia a trazione che a compressione. Ovvero di sezioni che non si parzializzano.
Solamente dopo si affronteranno le sezioni che si parzializzano a trazione.
Definiamo adesso le sollecitazioni agenti sulla sezione. Una tripletta di sollecitazioni, precisamente:
N, una forza disposta con direzione ortogonale al piano della sezione, essa avrà verso positivo se genera compressione nella sezione e negativo se genera trazione, e con punto di applicazione coincidente con il baricentro della sezione omogenea (senza considerare le armature);
Mx, un momento flettente con asse momento coincidente con l'asse x e con verso positivo se esso genera compressione nelle fibre della sezione disposte lungo il verso positivo dell'asse y (regola della mano sinistra);
My, un momento flettente con asse momento coincidente con l'asse y e con verso positivo se esso genera compressione nelle fibre della sezione disposte lungo il verso positivo dell'asse x (regola della mano destra).
Normalmente, per una sezione generica (ma reagente sia a compressione che a trazione) provvederemmo a determinare le caratteristiche geometriche della sezione, l'inclinazione degli assi principali rispetto agli assi coordinati, i momenti flettenti proiettati su questi assi, ed infine utilizzando una formula del tipo:
σ=N/A+Mbeta/Walfa+Malfa/Wbeta
Ricavare le massime tensioni nei punti 'critici' della sezione.
Si procederà invece per differente strada, senza passaggi di coordinate, forse più complicata da percorrere nel caso specifico, ma che consente tante possibilità in più, che potranno essere applicate successivamente alle sezioni parzializzate.
Ora, tutto il discorso non può esulare dalle solite, classiche, equazioni di equilibrio.
Nella loro forma più generale, introducendo la funzione σ(x,y) che rappresenta la tensione che agisce nel punto generico (x,y) della sezione:
∫σ(x,y)*dΩ+Σaf*σf(xa,ya)=N
∫σ(x,y)*y*dΩ+Σaf*σf(xa,ya)*ya=Mx
∫σ(x,y)*x*dΩ+Σaf*σf(xa,ya)*xa=My
Dove gli integrali sono estesi all'intera area Ω della sezione; e dove, attenzione, x ed y sono coordinate riferite ad un sistema di assi che ha origine nel baricentro della sezione omogenea (baricentro che è anche punto di applicazione di N). xa,ya sono le coordinate di ogni singola barra di armatura, sempre rispetto a questo sistema di assi.
In definitiva le tre equazioni messe a sistema indicano semplicemente che l'insieme delle tensioni che si instaurano punto per punto nella sezione devono essere in grado di equilibrare contemporaneamente lo sforzo normale esterno e i due momenti flettenti.
Fino a questo momento la generalità delle equazioni è tale che non è stato necessario fare alcuna ipotesi “restrittiva” su tensioni, comportamento della sezione sotto carico, ecc.
Dovendo arrivare ad una soluzione non generica, dobbiamo cominciare a farlo adesso.
Ovviamente trattasi delle ipotesi “classiche” che qui vengono richiamate:
1) Deformazione piana della sezione;
2) Elasticità lineare dei materiali costituenti la sezione.
Con questi due concetti essenziali, è possibile fare delle considerazioni che tolgono certamente generalità alle 3 equazioni scritte prima, ma che consentono anche di risolverle in maniera “comoda”.
Ci si concentri ora sulla deformazione della sezione. Ovvero sulla funzione deform(x,y) che ci restituisce la deformazione sotto carico nel generico punto x,y della sezione.
Per la prima ipotesi, visto che deformandosi la sezione deve rimanere piana, tale funzione dipende da tre soli parametri: una deformazione lineare in corrispondenza del baricentro della sezione, una rotazione della stessa attorno all'asse x (sempre baricentrico) ed una rotazione attorno all'asse y (sempre baricentrico).
In pratica la funzione avrà una espressione (ovviamente stiamo parlando di piccoli spostamenti e piccole rotazioni, tali da far ritenere tan(φx)=φx e tan(φy)=φy):
deform(x,y)=u+φx·y+φy·x
Le convenzioni riguardo questi tre parametri sono sostanzialmente identiche alle convenzioni sui segni esposte per le sollecitazioni esterne, pertanto:
u è una deformazione positiva se “comprime” la sezione.
φx è la rotazione attorno all'asse x, positiva se la parte di sezione in direzione +y si “comprime” (regola della mano sinistra).
φy è la rotazione attorno all'asse y, positiva se la parte di sezione in direzione +x si “comprime” (regola della mano destra).
(Notare che spostamenti e sollecitazioni esterne hanno le stesse convenzioni riguardo segni negativi o positivi).
Ma d'altra parte per la seconda ipotesi, la elasticità lineare del materiale, esiste una costante di linearità - il modulo elastico del materiale – che lega deformazione a tensione, per cui:
σ(x,y)=E*deform(x,y)
Ed in ultima analisi:
σ(x,y)=E*(u+φx*y+φy*x)
Sostituiamo quindi questa espressione alle tre equazioni di equilibrio.
(Ovviamente le armature hanno un differente modulo elastico e quindi per esse dovremo moltiplicare la funzione σ(x,y) per il coefficiente “omog” introdotto nella Parte 2)
Ecco cosa si ottiene:
E*[u*∫dΩ+φx*∫y*dΩ+φy*∫x*dΩ+omog*(u*Σaf+φx*y*Σaf+φy*x*Σaf)]=N
E*[u*∫y*dΩ+ φx*∫y2*dΩ+ φy*∫x*y*dΩ+omog*(u*y*Σaf+φx*y2*Σaf+φy*x*y*Σaf)]=Mx
E*[u*∫x*dΩ+ φx*∫x*y*dΩ+ φy*∫x2*dΩ+omog*(u*x*Σaf+φx*x*y*Σaf+φy*x2*Σaf)]=My
Nella prima equazione così riscritta, il primo integrale è l'area della sezione (considerando anche le armature), il secondo integrale è il momento statico attorno all'asse x, il terzo integrale il momento statico attorno all'asse y.
Ugualmente si potrà osservare riguardo alla seconda equazione, dove compaiono il momento statico attorno ad x, il momento d'inerzia attorno ad x, il momento d'inerzia x,y.
E nella terza equazione il momento statico attorno ad y, il momento d'inerzia x,y, il momento d'inerzia attorno all'asse y.
Pertanto le equazioni di equilibrio possono essere essere scritte nella seguente forma più compatta:
E*[Area*u+Sx*φx+Sy*φy]=N
E*[Sx*u+Jx*φx+Jxy*φy]=Mx
E*[Sy*u+Jxy*φx+Jy*φy]=Mx
In termini matriciali, individuando una matrice dei coefficienti (Area, Sx, ecc.) un vettore deformazione (u,φx,φy), ed infine un termine noto (N,Mx,My). In questo modo: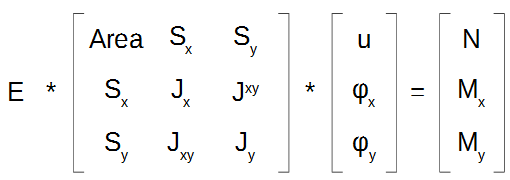
La matrice dei coefficienti prende anche il nome di “matrice di rigidezza della sezione”.
Essa infatti gode delle stesse proprietà di una matrice di rigidezza di strutture più complesse ad articolate. Area, Jx, Jy, i termini sulla diagonale, sono essenzialmente positivi, ed è anche simmetrica.
Tale sistema è risolvibile. Abbiamo tre equazioni di equilibrio e tre incognite (u,φx,φy), che, attraverso il termine noto (N,Mx,My), possono essere tranquillamente ricavate.
L'incomodo E può essere trascurato. Risolvendo il sistema, senza moltiplicare tutte le equazioni per E, non si trovano effettivamente le deformazioni della sezione, ma 3 numeri “ibridi”, che però, con la formula:
u+φx*y+φy*x
Darebbero, a meno del fattore “omog”, direttamente la tensione nel punto generico di coordinate x,y.
Per ricavare le massime o minime tensioni nella sezione basterà indagare le tensioni agenti sui vari vertici della stessa. Per le ipotesi fatte, i massimi e minimi possono annidarsi solamente in quei punti.
Riguardo il fattore “omog” l'unica accortezza sarà, nel caso di vuoti della sezione, di renderne positivo il valore, affinchè non si invertano tutti i segni delle tensioni nei vertici di un poligono vuoto.
L'algoritmo esula assolutamente dalla necessità di definire o di ricavare una posizione dell'asse neutro della sezione (asse che divide la parte tesa della sezione dalla parte compressa) per risolvere le equazioni di equilibrio. L'asse neutro può tranquillamente essere ricavato dal “campo” di tensioni che esce fuori dal calcolo, ma esso non serve affatto in sede di determinazione delle tensioni stesse.
Questo è un concetto importante per andare a trattare il caso delle sezioni che si parzializzano a trazione.. -
.
Parte 4
Le sezioni che si parzializzano - Verifica a presso flessione agli SLE
La difficoltà nel trattare le sezioni in c.a. (materiale che si parzializza) che non siano rettangolari e sollecitate con flessione retta deriva dal metodo normalmente messo in campo per giungere alla soluzione.
Nei testi su cui si studia ci si accorge subito della “fatica” con cui è possibile arrivare alle tensioni in sezioni, anche di semplice geometria, ma sollecitate a presso-flessione deviata. Costruzioni grafiche, artifici vari, e soprattutto l'onnipresente “asse neutro”.
Ovviamente vi chiederete come fare a meno dell'asse neutro, quella retta che separa la zona tesa dalla compressa, proprio in una sezione che si parzializza. Con il metodo proposto l'asse neutro sarà un risultato, non sarà l'input di partenza da cui far scaturire tutto.
Con questo semplice “ribaltamento” di pensiero le cose si semplificheranno parecchio.
Poiché il vero input come abbiamo già visto nella parte precedente, con il metodo della “matrice di rigidezza della sezione” rimane sempre una tripletta deformativa, ossia la formula principe rimane:
deform(x,y)=u+φx*y+φy*x
Questa con le precisazioni di cui alla parte 3, circa il valore di E da mettere da parte, coincide con il “campo” di tensioni agente sull'intera superficie della sezione. Sostituendo ad x ed y le coordinate di un qualsiasi vertice di un poligono della sezione (coordinate rispetto al baricentro della sezione omogenea), restituisce la tensione nel vertice stesso.
Pertanto il metodo visto nella parte 3 è perfettamente utilizzabile anche per le sezioni che si parzializzano. Basterà sostituire ai coefficienti della “matrice di rigidezza” le caratteristiche statiche della sola parte reagente di sezione, piuttosto che le caratteristiche della sezione intera come fatto finora, perchè il tutto continui a funzionare.
Piccolo, ma nemmeno tanto, granello di sabbia nel meccanismo che stiamo delineando: Ma se a priori non si sa come la sezione si parzializza, come calcolare le caratteristiche geometriche corrette?
La risposta risiede in un metodo che prevede delle iterazioni successive avvicinandosi alla soluzione del problema.
Bisogna partire da una tripletta di valori per (u,φx,φy) di primo tentativo, e poi procedere per iterazioni successive.
Qualcuno (non so chi) ha dimostrato che basta partire da una tripletta (1,0,0) perchè il problema sia sempre convergente (è vero!). Faccio notare che imporre u=1 e rotazioni nulle, significa di fatto non avere trazione (inizialmente) nella sezione e che quindi le varie caratteristiche geometriche della sezione “parzializzata” sono proprio quelle della sezione intera.
Lo schema di procedimento segue quindi questa sequenza:
1) Con la tripletta di primo tentativo (1,0,0) si determinano i coefficienti della matrice di rigidezza (quelli della sezione intera, quindi);
2) Con il termine noto dato dalle sollecitazioni si risolve il sistema lineare a tre incognite e tre equazioni, trovando una differente tripletta di valori per (u,φx,φy);
3) Con questi tre valori deformativi si è in grado di verificare quali vertici della sezione “intera” sono in trazione e quali in compressione;
4) Si definisce una nuova geometria per la sezione che comprende la sola parte compressa (le armature sono sempre presenti);
5) Si determinano nuovamente i coefficienti della matrice di rigidezza con la nuova geometria e si riparte con il passo 2.
In questo modo, a poco a poco, l'algoritmo proposto “aggiusta” la sezione. Per ogni tripletta deformativa ricavata la sezione modifica la sua forma, fino a quando la differenza tra la tripletta della iterazione n-1 e la iterazione n non diventa più piccola di un fattore di tolleranza imposto (oppure quando la differenza tra le aree della sezione reagente tra l'iterazione n-1 ed n non è inferiore ad un valore imposto).
Qui si proporrà la differenza in valore assoluto tra “norma” della tripletta n e tra la “norma” della tripletta n-1 sia inferiore a 0.001.
Per 'norma' si intende radq(u²+φx²+φy²).
Con 6-7 di queste iterazioni normalmente si arriva al risultato definitivo. Al massimo con 10. Da un punto di vista computazionale l'elaboratore perderà più tempo a ricalcolare ogni volta la matrice dei coefficienti che a risolvere il sistema (che ricordo essere un semplicissimo 3x3).
Alla fine il vero “problema” diventa riuscire a ricavare ad ogni iterazione i nuovi poligoni che rappresentano la sola parte compressa della sezione.
Nella seguente figura viene riportata la situazione alla iterazione i, del processo: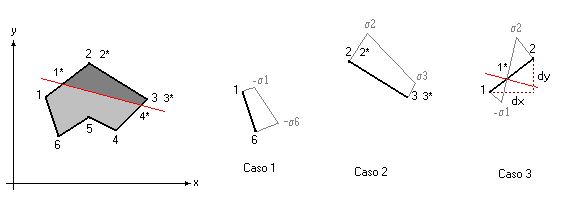
Non guardate la linea rossa (che separerebbe la parte compressa da quella tesa della sezione). Quello che conta sono i vari casi possibili riportati a destra.
Nella iterazione i si è quindi arrivati ad una tripletta data genericamente da (u, φx, φy). Con queste deformazioni (che poi sono tensioni) alcune parti della sezione verranno sollecitate a trazione, altre a compressione.
Analizziamo adesso quindi cosa succede su ogni lato dei nostri poligoni.
Il caso 1 riporta il lato 1-6 del poligono che rappresenta la sezione e che risulta essere sempre teso, pertanto esso non potrà far parte del nostro poligono “reagente”. Semplicemente esso si scarta. Quella parte di sezione non interessa;
Il caso 2, al contrario rappresenta il lato 2-3, che risulta essere sempre compresso. Questo lato, con i relativi vertici, farà parte del poligono “reagente”;
Il caso 3, infine è proprio quello di maggiore interesse. E' il lato 1-2 (ma il lato 3-4 ha la stessa situazione) che presenta il vertice 1 con tensione di trazione, il vertice 2 con tensione di compressione. E' ovvio che lì in mezzo, tra il vertice 1 e 2 si “anniderà” un punto di tensione 0.0 (la tensione varia linearmente da -σ1 a σ2 lungo il lato 1-2 per le ipotesi di partenza circa la deformazione piana della sezione e per il rapporto di linearità tra tensione e deformazione). E' proprio quel punto di tensione nulla che farà da confine per il nuovo poligono che deve rappresentate la sola parte compressa della sezione. Esso quindi sarà un “nuovo” vertice del poligono. Nella figura ho rappresentato con 1*, 2*, 3*, 4* il nuovo poligono “compresso” di cui calcolare le caratteristiche statiche per la successiva iterazione di calcolo.
Le coordinate del nuovo vertice 1*, con considerazioni semplici di rapporti tra triangoli (vedi figura), e considerando i valori delle tensioni nel loro valore assoluto (senza segno), sono esprimibili con le formuline:
x1*=x1+σ1*(x2-x1)/(σ1+σ2)
y1*=y1+σ1*(y2-y1)/(σ1+σ2)
Se poi siamo affezionati ai segni:
x1*=x1-σ1*(x2-x1)/(σ2-σ1)
y1*=y1-σ1*(y2-y1)/(σ2-σ1)
E faccio notare come questa formula funziona anche se σ1 è positivo e σ2 è negativo (ovvero 1 è vertice compresso e 2 vertice teso), poiché il numeratore (σ1) cambia segno, ma anche il denominatore (σ2-σ1).
Esaminiamo casi particolari che possono verificarsi nella divisione in due (parte compressa, parte tesa) della sezione. Prendiamo ad esempio questa figura: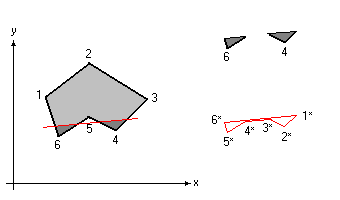
Se la parte compressa fosse quella inferiore, il singolo poligono che rappresenta la sezione dovrebbe potersi scomporre nei due singoli poligoni rappresentati in alto a destra nella stessa figura. Oppure potrebbe scomporsi anche in più di poligoni.
Non si tratta di un problema se il poligono compresso viene rappresentato come nel contorno in rosso. Si tratta sempre di un solo poligono, in cui il lato 3*-4* “giace” sul lato 6*-1*.
Per gli algoritmi di calcolo delle caratteristiche statiche, presentati nella parte 1, dare in pasto il doppio poligono (sopra) o il poligono “quasi intrecciato” (sotto) non fa alcuna differenza. I numeri rimarrebbero gli stessi.
In definitiva la soluzione del problema, da un punto di vista computazionale, si ottiene semplicemente con la implementazione di una funzione che itera n volte la soluzione del sistema 3x3 individuato nella parte 2, e con una ulteriore funzione che si occupa di riempire la matrice dei coefficienti del sistema 3x3 con i valori corretti.. -
.
Parte 5
Verifiche SLU – Si comincia
La verifica SLU consisterà nel determinare il dominio di rottura nel piano Mx-My dato un determinato Nd agente sulla sezione.
Pur considerando la sezione del tutto generica si procede inizialmente con due ben precise assunzioni:
- Asse neutro orizzontale;
- Zona compressa della sezione al di sopra dell'asse neutro;
Successivamente si vedrà come quanto sviluppato con queste assunzioni possa essere facilmente esteso per riuscire a ricavare la “fetta di salame” nel piano Mx-My che rappresenta il dominio di rottura della sezione (per dato Nd).
In questo modo si semplificano le equazioni di geometria analitica da trattare. Ad esempio sarà possibile individuare i vertici compressi della sezione semplicemente controllando se la loro ascissa y è maggiore della ascissa yn dell'asse neutro. Così come sarà facile trovare il vertice compresso più distante dall'asse neutro (o la barra di armatura in trazione più distante dall'asse neutro).
Nella figura sottostante uno schema per definire la situazione geometrica da indagare: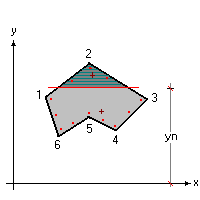
Le crocette in rosso scuro rappresentano le risultanti degli sforzi di compressione e di trazione. Il prodotto dello sforzo Nd per la distanza tra questi due punti definisce il momento di rottura. Se invece della distanza si moltiplica per dy e dx (proiezioni sugli assi coordinati della distanza tra le risultanti) si ottengono rispettivamente i momenti Mrx ed Mry.
La posizione dell'asse neutro viene fatta variare iterativamente fino a quanto la somma algebrica tra la risultante di compressione della zona compressa e la risultante di trazione delle armature tese non sia proprio pari ad Nd.
Definita una posizione qualsiasi dell'asse neutro, sarà possibile, subito, ricavare la configurazione deformativa a rottura assunta dalla sezione.
Nel seguente diagramma, le possibili situazioni previste: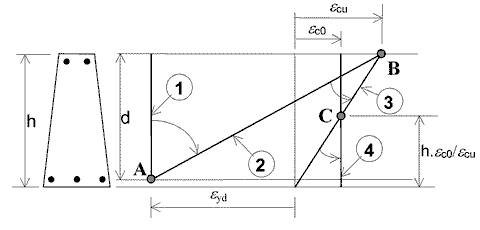
Definiamo:
yn: ordinata dell'asse neutro;
ymax: massima ordinata tra tutti i vertici della sezione;
yamin: minima ordinata tra tutte le barre di armatura;
εa: deformazione in corrispondenza di ymax;
εb: deformazione in corrispondenza di yamin;
εyd: deformazione massima dell'acciaio (valore negativo se di trazione);
εcu: deformazione massima nel calcestruzzo (valore positivo se di compressione)
εc0: deformazione in cui termina il tratto parabolico del “classico” diagramma parabola-rettangolo
Conoscendo le deformazioni in ymax ed yamin, per l'ipotesi di conservazione della planarità, si ricava la deformazione in qualsiasi altra fibra della sezione. Infatti per ogni fibra posta alla generica quota y, si avrà:
ε=εa+(εb-εa)*(ymax-y)/(ymax-yamin)
Dove εb e εa vanno inseriti con il loro effettivo segno nella formula.
Le situazioni che possono riscontrarsi guardando la figura sono solamente tre, ovvero:
a) Posizione dell'asse neutro: +∞>yn>(│εyd│*ymax+εcu*yamin)/(εcu+│εyd│) (Settore 1-2 in figura)
In questo caso:
εb=εyd (valore negativo)
εa=εyd*(yn-ymax)/(yn-yamin)
Ad εyd viene assegnato il valore -0.0675 (pari al 90% di 7.5% deformazione a rottura di un acciaio B450C – vedi §4.1.2.1.2.3 e Tab. 11.3.Ib)
b) Posizione dell'asse neutro (│εyd│*ymax+εcu*yamin)/(εcu+│εyd│)≥yn>yamin (Settore 2-3 in figura)
In questo caso:
εa=εcu
εb=εcu*(yn-yamin)/(yn-ymax)
c) Posizione dell'asse neutro yamin≥yn>-∞ (Settore 3-4 in figura)
In questo caso il diagramma ruota attorno al punto di deformazione εc0 posto a quota yc0=yamin+εc0*(ymax-yamin)/εcu, e quindi:
εa=εc0*(ymax-yn)/(yc0-yn)
εb=εc0*(yamin-yn)/(yc0-yn)
Si è dato un valore numerico alla sola deformazione massima εyd, lasciando le altre grandezze “indefinite”. Perchè in questo interviene la normativa che prevede differenti valori di εc0 ed εcu per i calcestruzzi con classe di resistenza superiore a C50/60 (vedi §4.1.2.1.2.2 del D.M. 14/01/2008).
Una volta definita la deformazione a qualsiasi 'altezza' della sezione, tramite i legami costitutivi dei materiali (cls ed acciaio) è possibile ottenere la tensione in ogni punto della sezione.
Ovviamente si farà riferimento ai diagrammi di normativa. Specificamente al diagramma parabola-rettangolo per il calcestruzzo, ed al diagramma elasto-plastico lineare con incrudimento per l'acciaio.
Ma essi verranno 'adimensionalizzati' in modo da poterli sempre utilizzare anche con poligoni di differenti caratteristiche di calcestruzzo, o con barre di differenti tipologie di acciaio.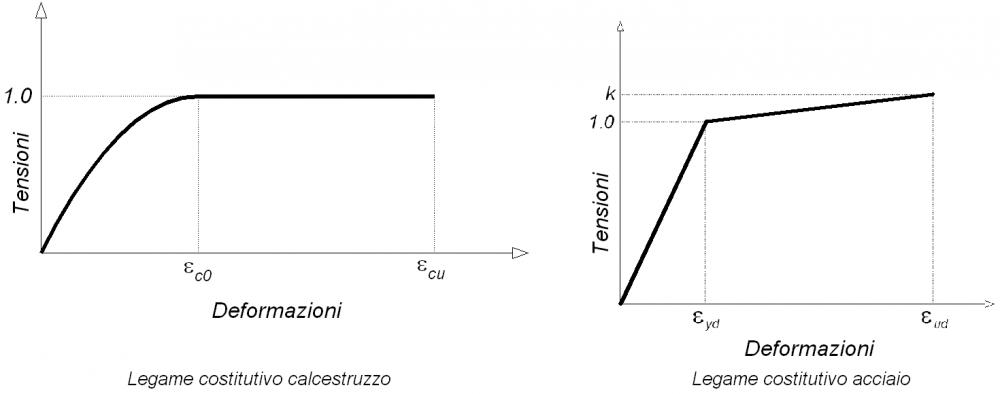
Nel caso del calcestruzzo, con la deformazione della singola fibra compressa, il diagramma adimensionalizzato restituirà un valore compreso tra 0 ed 1, che moltiplicato per fcd darà proprio la tensione nella fibra.
Identicamente si procede per le barre di armatura. Nel diagramma adimensionalizzato entrando con una deformazione, si ottiene un valore compreso tra 0 e k (k=rapporto di incrudimento dell'acciaio, generalmente compreso tra 1.15 ed 1.35 per un acciaio B450C, inferiore ad 1.05 per un acciaio B450A), anche in questo caso moltiplicando tale valore per fyd si ottiene la tensione nella barra.
Nel diagramma parabola-rettangolo la parte parabolica viene espressa con una legge del tipo:
y=a·x2+b·x+c
I parametri a, b e c si ottengono dal passaggio della parabola per i punti 0;0 e εc0;1 ed imponendo la tangenza orizzontale in questo ultimo punto.
Ottenendo i parametri della parabola: a=-1/εco2 , b=2/εc0 , c=0.
Nel diagramma incrudente dell'acciaio, superando la tensione di snervamento, la tensione restituita dal diagramma per dato ε sarà:
1.0+(ε-εdy)*(k-1)/(εud-εyd)
Per ottenere la risultante N della parte compressa della sezione si procederà a suddividere in striscie 'sottili' tutta la parte di sezione al di sopra dell'asse neutro.
- Per ogni quota a cui si trova la mezzeria della striscia si determinerà la deformazione;
- dalla deformazione, tramite il legame costitutivo si risalirà alla tensione;
- la tensione moltiplicata per altezza e larghezza della striscia, determina lo sforzo normale esercitato dalla striscia dN
- la sommatoria dei contributi dN su tutte le striscie definisce lo sforzo di compressione complessivo sulla zona compressa della sezione.
A questo valore di Nc si aggiungeranno anche le singole forze esercitate dalle barre compresse di armatura.
Quindi riepilogando, la procedura proposta sarà di tipo iterativo. Posizionato l'asse neutro in una generica posizione si determinerà:
1) Una configurazione deformata di “rottura” della sezione;
2) Determinazione dello sforzo normale della parte compressa della sezione (Nc);
3) Determinazione dello sforzo di trazione complessivo esercitato dalle armature (Nt);
4) Controllo che la somma algebrica Nc+Nt sia proprio Nd. Altrimenti si modifica la posizione dell'asse neutro e si ricominca da 1;
I momenti Mx ed My di rottura corrispondenti ad Nd (rispetto al baricentro della sezione omogenea), verranno determinati conoscendo la posizione delle risultanti di compressione Nc e di trazione Nt.
Circa la effettiva configurazione deformativa a rottura bisogna però spendere ancora qualche parola, visto che la sezione è costituita non da uno ma da più poligoni.
Infatti, se la sezione è costituita da più poligoni, e se alcuni di questi poligoni sono costituiti da calcestruzzo con classe di resistenza superiore a C50/60, e quindi con valori di εcu ed εc0 differenti dai soliti 3.5 per mille (minore di tale valore) e 2 per mille (maggiore di tale valore), bisognerà garantire che la deformazione in ymax del 3.5 per mille (poiché per esempio ymax è di un vertice appartenente ad un poligono “normale”) sia compatibile con la massima deformazione possibile di un vertice del poligono “special”, magari posto pochi centimetri più in basso di ymax.
Nella figura successiva viene presentato proprio il caso cui si sta accennando: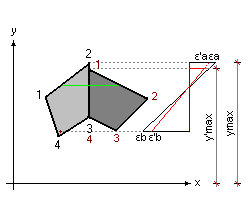
Chiaramente, quando si definiscono le deformazioni limite della sezione, si dovrà tenere conto del problema.
La deformata che “comanda” a questo punto è quella del poligono “forte” (quello più scuro della figura), e questo dovrà rispettare le condizioni a) b) o c) comunque (massima tensione di rottura in un lembo piuttosto che nell'altro).
Però gli effettivi casi che possono realmente verificarsi sono il b) (in quanto al lembo superiore si ha già una deformazione limite, il materiale cls) oppure il c).
Allora, per il caso b) le nuove deformazioni, indicate con ε'a ed ε'b in figura, valgono:
ε'a=ε'cu*(ymax-yn)/(y'max-yn)
ε'b=ε'cu*(yn-yamin)/(yn-y'max)
Invece nel caso c) si modifica anche il punto di rotazione della sezione, ovvero:
y'c0=yamin+ε'c0*(y'max-yamin)/ε'cu, e quindi:
ε'a=ε'c0*(ymax-yn)/(y'c0-yn)
ε'b=ε'c0*(yamin-yn)/(y'c0-yn)
Questi controlli di “congruenza” vanno estesi a tutti i poligoni che costituiscono la sezione, ritoccando di volta in volta i numeri. Certamente è uno ed uno solo il poligono che “comanda”.. -
.
Parte 6
Larghezza delle fibre e loro baricentro
Come visto nella parte precedente un 'tassello' importante per la determinazione dello sforzo normale di compressione agente sulla sezione è la larghezza di ogni singola fibra in cui si pensa di suddividere la sua parte compressa.
Considerando come già detto l'ipotesi di asse neutro sempre orizzontale, con un po' di geometria analitica bisognerà semplicemente valutare le intersezioni della retta y=yf (con yf la ordinata della fibra di interesse) con il perimetro di uno dei poligoni.
Prima bisognerà però svolgere alcune considerazioni “topologiche”.
La situazione standard infatti è quella della figura a sinistra: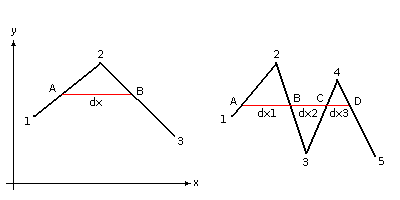
Un po' più articolato è quanto accade, invece, nella parte destra della stessa figura. Infine, ecco il caso più “complesso” che possa capitare: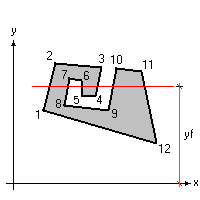
In ogni caso si vede che la retta y=yf interseca (se lo fa) un singolo poligono, sempre in un numero pari di punti (n), staccando un numero dispari di segmenti (n-1). Si vede anche come la lunghezza complessiva della fibra sia la somma delle lunghezze dei segmenti dispari.
Vediamo di ricavare le coordinate delle intersezioni tra retta y=yf e poligono. Prendiamo un singolo segmento, come in figura: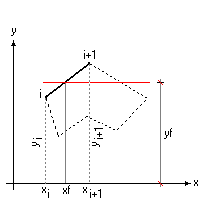
Il segmento i / i+1 ha una equazione y=m·x+q, dove:
m=(yi+1-yi)/(xi+1-xi)
q=yi-m*xi
Mettendo a sistema le due equazioni:
y=m·x+q
y=yf
si ottiene per xf:
xf=(yf-q)/m
Adesso sostituendo ai vari simboli le espressioni, ricaviamo questa espressione per xf un po' articolata:
xf=[(yf-yi)*(xi+1-xi)+(yi+1-yi)*xi /(yi+1-yi)
Ma che consente di non dover gestire il caso particolare di segmento del poligono perfettamente verticale (che avrebbe m, coefficiente angolare, infinito). La formula cadrebbe in difetto nel caso di segmento orizzontale (yi+1-yi diventa nullo), ma due rette orizzontali....si incontrano all'infinito comunque.
Per risolvere la questione basterà non processare, dunque, tutti i segmenti orizzontali.
Adesso quindi, facendo il giro, segmento per segmento del poligono, si troveranno tutte le coordinate xf di intersezione del poligono con la retta y=yf.
E' importante far notare (la figura con il caso “complesso” ne è un esempio), che le coordinate xf non vengono ricavate sempre in maniera crescente, ma a “casaccio”. Può accadere anche nel caso semplice di normale doppia intersezione. Dipende infatti da quale è il primo lato del poligono.
Pertanto dopo aver ricavato tutte le xf bisognerà procedere al loro ordinamento crescente, in modo da poter procedere quindi alla definizione della lunghezza della fibra, che ricordo consiste nel sommare le lunghezze dei segmenti dispari (quindi xf2-xf1 e xf4-xf3 e xf6-xf5, ecc.).
Dalla lettura della parte 5 quello che ci serve per i calcoli successivi non è solamente la larghezza della fibra (necessaria per definire un N), ma anche il baricentro di questa serie di segmenti (necessari, trovato l'N voluto, a definire i momenti di rottura della sezione).
Pertanto la funzione che calcola la lunghezza della fibra dovrà restituirmi anche la coordinata xb di tale punto.
Considerando un singolo segmento di coordinate iniziali e finali rispettivamente xf2 ed xf1, ecco che il baricentro sarà posizionato a xb=(xf2+xf1)/2.
Nel caso di più segmenti nella stessa fibra, il baricentro sarà posizionato:
xfg=[Σ(xf2+xf1)/2*(xf2-xf1)]/ Σ(xf2-xf1)
Dove la sommatoria è estesa al numero di segmenti riscontrati.. -
.
Parte 7
Risultanti di compressione e di trazione
Rapido riepilogo:
- si fissa la posizione dell'asse neutro;
- dalla posizione dell'asse neutro si determinano le deformazioni a rottura in qualsiasi porzione della sezione;
- si determina la risultante della zona compressa;
- si determina la risultante della zona tesa;
- si controlla che la somma algebrica delle due risultanti sia pari a Nd
Per la determinazione della risultante della zona compressa abbiamo visto che dividendo in sottili strisce orizzontali la sezione siamo in grado di ricavare il dN 'offerto' da ciascuna striscia, ed anche la posizione in orizzontale della risultante di questo dN (la posizione in verticale è ovviamente la ascissa yi del centro della fibra).
Pertanto la sommatoria di tutti questi contributi darà proprio la risultante Nc della parte compressa.
Ovviamente se yn (ascissa dell'asse neutro) dovesse essere maggiore del punto più alto della sezione è evidente che nessuna porzione della sezione è in compressione e pertanto Nc=0.
Per quanto riguarda la determinazione del punto di applicazione di questa forza bisognerà determinare il momento statico della distribuzione con la semplice sommatoria di tutti i contributi delle singole strisce:
Scx=ΣdNi·yi
Scy=ΣdNi·xi
Dove yi è l'ascissa alla metà dello spessore della striscia considerata e xi la coordinata del baricentro della striscia.
Evidentemente si avrà:
xr-compr=Scy/Nc
yr-compr=Scx/Nc
Le suddette coordinate sono riferite al sistema di riferimento generale a cui sono riferiti tutti i vertici della sezione.
Aumentando la “finezza” delle strisce si migliora la precisione numerica del risultato, ma si rallenterebbe la velocità di elaborazione. Il criterio potrebbe essere quello di limitare in un certo range la larghezza della singola striscia (da 0.5 a 2 mm). In questo modo il numero di suddivisioni risulta essere ottimizzato in funzione della 'profondità' della porzione compressa di sezione, senza inficiare i risultati numerici.
Per quanto riguarda le armature in trazione il discorso è analogo.
Determinata la deformazione di ogni singola barra si è in grado, tramite il legame costitutivo di poter determinare la tensione (quindi moltiplicando per Af, la forza) di ogni singola barra.
La sommatoria di tutte le forze esplicate da ogni barra sarà pari ad Nt.
Il baricentro, come al solito si ricaverà dai momenti statici:
Stx=ΣFi·yi
Sty=ΣFi·xi
Dove Fi, xi ed yi sono rispettivamente la forza e le coordinate di ogni singola barra tesa di armatura.
Evidentemente si avrà:
xr-traz=Sty/Nt
yr-traz=Stx/Nt
Evidentemente se nessuna armatura fosse tesa il valore di Nt sarebbe nullo.
Le barre di armatura che invece avessero deformazione di compressione contribuiranno ad incrementare il valore di Nc, e con le stesse formule entreranno in gioco per la determinazione della posizione della risultante di compressione.. -
.
Parte 8
La determinazione dell'asse neutro
E' chiaro che la ricerca della posizione dell'asse neutro deve avvenire per via iterativa. Si stabilisce una posizione dell'asse neutro, si ricavano le risultanti di compressione e trazione, e si controlla che la loro somma algebrica sia pari ad Nd. Se così non è si sposta l'asse neutro e si prova nella nuova configurazione geometrica.
Ovviamente bisognerà rendere intelligente una simile ricerca considerando che la posizione effettiva dell'asse neutro può anche andare da un massimo di +∞ ad un minino di -∞.
Si potrebbe operare con il classico metodo della bisezione. Si determina lo squilibrio rispetto ad Nd con un paio di posizioni dell'asse neutro, e con semplici considerazioni 'lineari' si può stabilire la terza posizione dell'asse neutro, via via fino a rendere la differenza tra Nd ed il valore calcolato inferiore ad una tolleranza prefissata.
Nelle funzioni sviluppate la ricerca della posizione dell'asse neutro viene svolta “a passo variabile”.
Un semplice esempio chiarirà la metodologia seguita.
Immaginiamo che Nd sia 10000 e che da un primo tentativo di posizionamento dell'asse neutro, la somma algebrica di N compressione ed N trazione nella sezione sia pari a 7000.
Risulta evidente che bisogna aumentare la parte compressa di cls per arrivare ad Nd. Aumento che potrà avvenire posizionando più in basso l'asse neutro di una quantità “delta”. Da questa nuova posizione, ricalcolando il tutto si ottenga una risultante nella sezione di 11000. Ecco quindi che avendo superato Nd la posizione effettiva dell'asse neutro si trova in mezzo al tratto “delta”. A questo punto si riduce il passo “delta” (ad esempio della metà, ad un terzo, ecc.) e si “torna indietro” sui propri passi (invertendo di segno il valore delta), ed ogni volta che accade che la differenza tra Nd ed N calcolato della sezione varia di segno si riduco ulteriormente il passo “delta” di variazione dell'asse neutro (ed il suo segno). Il tutto fino ad ottenere una differenza minima tra Nd ed N calcolato, oppure un passo delta realmente microscopico.. -
.
Parte 9
Il dominio di rottura
Come si era detto proprio ad inizio trattazione delle verifiche SLU, il dominio di rottura verrà ricavato da coppie di mrx,mry calcolate non già facendo ruotare l'asse neutro, ma facendo ruotare fittiziamente la sezione stessa.
Vista la genericità dei concetti e delle espressioni che abbiamo via via ricavato, esse continueranno ad essere valide qualsiasi sia l'inclinazione della sezione rispetto agli assi coordinati.
In ogni caso l'asse neutro sarà considerato orizzontale (e con porzione compressa della sezione al di sopra dell'asse neutro).
Ovviamente una volta ricavati i valori di mrx ed mry per una certa rotazione fittizia assegnata alla sezione, si dovranno ricondurre questi momenti agli assi di riferimento X-Y effettivi della sezione originaria.
Ricavate le coordinate della risultante di sforzi normale di compressione e trazione, queste ultime devono essere riportate al primigenio sistema di riferimento per determinare i momenti di rottura (che ad unico sistema devono essere riferiti).
Ci servono quindi le formule per la trasformazione delle coordinate dei vertici e delle armature costituenti i vari poligoni della sezione.
Nell'immagine inferiore, lo schema geometrico dell'operazione più generale possibile, ovvero la roto-traslazione: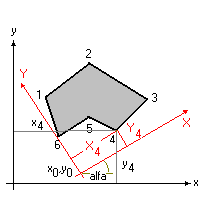
Il problema è risolvibile per via geometrica-trigonometrica e permette di ricavare le “nuove” coordinate X,Y dei vertici (in maiuscolo), semplicemente conoscendo le coordinate della origine del nuovo sistema di riferimento, rispetto al vecchio, e la rotazione degli assi.
Le formule generali per la roto-traslazione sono le seguenti:
X= x·cos(alfa)+y·sen(alfa)-x0
Y=-x·sen(alfa)+y·cos(alfa)-y0
Se l'operazione è di semplice rotazione del sistema di riferimento ecco che nelle formule di cui sopra scompaiono i fattori x0 ed y0 solamente.
E questo sembrerebbe tutto. Nel senso che basta fare questo per ottenere svariati punti del dominio di rottura della sezione per dato Nd.
Ovviamente si potrà seguire l'intero procedimento per tutte le combinazioni di carico cui è sottoposta la sezione, o magari procedere ad Nd via via crescenti per ottenere più “fette di salame” sovrapposte in modo da poter diagrammare in 3D la “safe ball” come la chiamano gli inglesi, ecc.
Ma proprio a questo proposito dobbiamo chiarire un ultimissimo aspetto, accennato in qualche commento, ma ancora da affrontare. Ovvero che non tutti gli Nd sono “buoni” e che non da tutti è possibile ricavare la “fetta di salame”. Ci saranno in effetti un valore di sforzo normale di compressione ed uno di trazione “limite” oltre i quali il dominio di rottura non esiste.
L'Nd massimo di trazione, oltre il quale la sezione non è in grado di spingersi, è dato dal prodotto dell'area complessiva delle barre di armature per fyd. Viceversa l'Nd massimo di compressione è dato dalla sommatoria di tutte le aree dei singoli poligoni per il rispettivo fd, e dall'area totale della barre per fyd, e questo poiché al minimo la sezione è uniformemente deformata del 2 per mille – alcuni contorni di cls particolarmente “buono” come abbiamo visto possono giungere a valori di deformazione limite più alti (vedi formule di normativa) – e con quella deformazione l'acciaio con modulo elastico 2100000 daN/cm² è già snervato (infatti 3913/2100000=0.00186).
Ma in ogni caso e per ogni evenienza è bene fare qualche controllo visto che i numeri possono anche essere differenti da quelli previsti (fyd maggiori di acciai migliori).. -
marco42.
User deleted
Salve.Volevo chiedere se il suddetto programma calcola le tensioni in sle anche in tenso-flessione.
grazie. -
.
Si. . -
.
Buongiorno, ho provato a implementare il tuo codice per calcolare i momenti di inerzia principali di una sezione qualsiasi. Mentre nel caso di Ixx ed Iyy ho capito come sono state ricavate le formule e sono riuscito ad implementarlo con successo, nel caso del momento di inerzia centrifugo non sono riuscito ne a implementare la formula ne a capire come sia stata ricavata. In particolare non riesco a capire che cosa sia il parametro hy. Questo è l'unico parametro che non è stato illustrato ne nella spiegazione precedente ne nei disegni
Condivido con te la formula di cui vorrei delle delucidazioni. Grazie in anticipo
a*(x[i]/2*(y[i]2+d2/3+d*hy)+a/2*(y[i]2/2+d2/4+2*d*hy/3)). -
.
Si, scusami Jeffr, mi avevi inviato un MP e ti avevo risposto in maniera fuorviante (non avevo capito quale fosse il tuo dubbio).
Riguardando il codice vedo che il parametro hy è quello che nel mio codice corrisponde ad y[i].
Nello scrivere il post avevo tradotto il codice in modo che la formula fosse conforme alla figura e non mi sono accorto di aver "tradotto" solamente una parte. Che figura..........
Non chiedermi adesso da dove arriva la formula in questione perchè non lo ricordo affatto. In ogni caso corretta è così:
a*(x[i]/2*(y[i]2+d2/3+d*y[i])+a/2*(y[i]2/2+d2/4+2*d*y[i]/3))
Edited by zax2013 - 20/9/2022, 11:00.
La teoria che mancava |